# 递归-迷宫问题

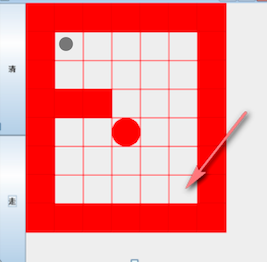
迷宫问题（回溯），上图说明：

红色的方块是围墙，是小球不能够走的
白色的方块是小球可以活动的范围
左上角是小球的起点，移动到右下角，就算走出了迷宫

那么在这个场景中，就用到了递归（Recursion），下面使用代码来实现小球走出迷宫的路径，学习数据结构，没有必要写界面。

package cn.mrcode.study.dsalgtutorialdemo.datastructure.recursion.maze;

import org.junit.Test;

/**
 * <pre>
 * 迷宫问题求解
 * </pre>
 */
public class Maze {
    @Test
    public void demo() {
        // 构建一个 8 行 7 列的地图
        int[][] map = initMap(8, 7);
        printMap(map);
        // 一次性没有回溯的路线
        setWay(map, 1, 1, 6, 5);
//         这个点，是有回溯的路线
//        setWay(map, 1, 1, 4, 1);
        System.out.println("路线查找完毕");
        printMap(map);
    }

    /**
     * <pre>
     *  思路说明：
     *  1. 从 startX,startY 开始走，到 endX,endY 结束
     *  2. 当走到 endX,endY 时，表示已经找到了路线
     *  3. 约定：map 中的含义：
     *      0：表示该点没有走过
     *      1：表示围墙，不能走
     *      2：表示改点已走过，并且可以走
     *      3：表示改点已走过，但是走不通
     *
     *  4. 走迷宫，约定一个寻找路线的策略，也就是当你站在一个点的时候，你从哪一个方向开始探索？
     *     这里规定探索的方向为：下 -> 右 -> 上 -> 左，如果该点走不通，再回溯
     * </pre>
     *
     * @param map    代表一张地图
     * @param startX 从哪一个点开始走
     * @param startY
     * @param endX   到哪一个点结束
     * @param endY
     * @return true: 表示该点可以走，false：表示改点不能走
     */
    public boolean setWay(int[][] map, int startX, int startY, int endX, int endY) {
        // 如果当结束点已经走过，表示已经到达了出口
//        System.out.println();
//        printMap(map); // 打开这个可以看到每一步的探索路径
        if (map[endX][endY] == 2) {
            return true;
        }
        // 那么开始我们的策略探索

        // 如果该点还没有走过，则可以尝试探索
        if (map[startX][startY] == 0) {
            // 先假定该点标可以通过，因为要去探索四周的点是否可以走
            map[startX][startY] = 2;
            // 下 -> 右 -> 上 -> 左
            // 根据策略：先往下走，如果可以走则返回 true
            if (setWay(map, startX + 1, startY, endX, endY)) {
                return true;
            }
            // 如果走不通，则继续往右边探索
            else if (setWay(map, startX, startY + 1, endX, endY)) {
                return true;
            }
            // 如果走不通，则继续往上边探索
            else if (setWay(map, startX - 1, startY, endX, endY)) {
                return true;
            }
            // 如果走不通，则继续往左边探索
            else if (setWay(map, startX, startY - 1, endX, endY)) {
                return true;
            }
            // 都走不通，表示改点是一个死点，四周都无法出去
            else {
                map[startX][startY] = 3;
                return false;
            }
        } else {
            // 如果不为 0，可能的情况是：1，2，3，这三种表示都表示不可以走
            return false;
        }
    }

    /**
     * 构建一个有挡板的地图
     * <pre>
     * 数字 1：表示挡板围墙，小球不可以经过
     * 数字 0：表示是路，小球可以经过
     * 起点：可以自定义起点
     * 出口：其实也可以自定义出口，但是本题规定，出口就是右下角的 0
     * 1 1 1 1 1 1 1
     * 1 0 0 0 0 0 1
     * 1 0 0 0 0 0 1
     * 1 1 1 0 0 0 1
     * 1 0 0 0 0 0 1
     * 1 0 0 0 0 0 1
     * 1 0 0 0 0 0 1
     * 1 1 1 1 1 1 1
     * </pre>
     *
     * @return
     */
    private int[][] initMap(int row, int cloum) {
        // 构建一个 8 行 7 列的地图
        int[][] map = new int[row][cloum];
        // 数字 1 表示挡板，构建一个有挡板的地图

        for (int i = 0; i < map[0].length; i++) {
            map[0][i] = 1;  // 顶部增加挡板
            map[map.length - 1][i] = 1;  // 底部增加挡板
        }

        for (int i = 0; i < map.length; i++) {
            map[i][0] = 1;  // 左侧增加挡板
            map[i][map[0].length - 1] = 1; // 右侧增加挡板
        }

        // 中间的其他固定挡板
        map[3][1] = 1;
        map[3][2] = 1;
        return map;
    }

    public void printMap(int[][] map) {
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[0].length; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136

我们先来看这个测试用例 setWay(map, 1, 1, 6, 5);，就是从左上角开始走，到右下角结束，输出的信息如下

1 1 1 1 1 1 1 
1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 1 1 0 0 0 1 
1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 1 1 1 1 1 1 
路线查找完毕
1 1 1 1 1 1 1 
1 2 0 0 0 0 1 
1 2 2 2 0 0 1 
1 1 1 2 0 0 1 
1 0 0 2 0 0 1 
1 0 0 2 0 0 1 
1 0 0 2 2 2 1 
1 1 1 1 1 1 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

这里看不出来有回溯的痕迹，其实根据我们的这个策略 下 -> 右 -> 上 -> 左，进入方法就打印 map 分布图，你就会发现，他去判断了墙壁的时候，回溯了一小步。但是还是不明显。

下面看一个回溯明显的路线

setWay(map, 1, 1, 4, 1);，从左上角，走到中间那个挡板的下面一个格子

1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 1 1 0 0 0 1 
1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 0 0 0 0 0 1 
1 1 1 1 1 1 1 
路线查找完毕
1 1 1 1 1 1 1 
1 2 3 3 3 3 1 
1 2 2 2 3 3 1 
1 1 1 2 3 3 1 
1 2 2 2 3 3 1 
1 0 2 2 3 3 1 
1 0 2 2 3 3 1 
1 1 1 1 1 1 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

可以看到，很多路线都被标识为了 3 ，走不通，按照我们手动来走，其实这些是能走通的，但是根据我们的策略来看，下 -> 右 -> 上 -> 左，先走下，再右，再上：

那么右侧区域全部都会走通，全部会被标识为 2
因为还没有走到出口，所以还会继续探索，当根据策略走到下一个点时，发现已经是 2 了，算法返回了 false，那么就会标记这个点不能走通，由 2 改成 3
上面的回溯会一直进行，由于是递归，最后会回到最底部的 2，然后根据策略会往左边走，才找到正确的路线

这个流程，打开每个步骤的路线分布图，就看的很明白了。

# 最短路径

上面实现的算法有一个问题，最短路径问题，经过上面的代码实现和测试之后，就会发现，怎么走，是根据我们的测量来走的，目前没有学习其他寻找最短路径的算法时，我们能做的也只有修改策略，比如出口在左下，那么我们就先往左下走。

← 递归入门递归-八皇后问题（回溯算法） →