斐波那契查找算法

基本介绍

黄金分割 点是指把一条 线段 分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近视值是 0.618。由于按此比例设计的造型十分美丽，因此称为 黄金分割，也称为 中外比。这是一个神奇的数字，会带来意想不到的效果。

简单说，两条线的比例为 1:1.618，比如上图的头和身体的比例、鼻子和嘴巴下巴的比例

斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } 发现斐波那契数列的 两个相邻数的比例，无限接近 黄金分割值 0.618

简单说：

3/2=1.5 、5/3=1.667、8/5=1.6、13/8=1.625 这样看来，他们的比例值是无限接近的 1.618 的
1/2=0.5 、3/5=0.6、5/8=0.625、8/13=0.6125 这样看，他们的比例值是无限接近  0.618 的

工作原理

与前两种（二分查找）类似，只是改变了 mid 值

要从这个数组 arr = {1, 8, 10, 1000} 中查找数值 1000
斐波那契数列：{1, 1, 2, 3, 5, 8, 13, 21, 34, 55 }
1. 在斐波那契数列中找到符合这个数组长度的数值，如果没有，则找最近的一个
   arr.length = 4, 在斐波那契数列中，没有 4 这个值，最近的一个是数值 5 ，index = 4
   那么 k = 4
2. 要将原数组的长度扩充为这个 k 对应的数值 5，多余出来的 1 个数字用原数组 arr 的最后一个值填充
   也就是：
      arr = {1, 8, 10, 1000}  扩充成如下
   newArr = {1, 8, 10, 1000,1000}
3. 计算 mid 值

他的公式是 mid = low + F(k-1) -1

怎么理解呢？由上述所知，k = 4，

{1,  1,  2,  3,  5, 8, 13, 21, 34, 55 }
                 ↑
             ↑   k
         ↑  k-1
        k-2

斐波那契数列的特性是除了相邻数的比例是无限接近黄金分割值，还有一个特性是：相邻的两个数相加等于后一个数

就如上所述： 2 + 3 = 5 ，3 + 5 = 8；那么其中变量解释如下：

• mid ：就是我们要对比的值索引
• low：该线段的最左端
• F(k-1) 和 F(k-2)：分别表示这个数组个数左右两端的个数各是多少

那么 arr = {1, 8, 10, 1000} 的长度是 4，补充为斐波那契数列中的值后，新的数组长度是 5

k = 4
{1,  1,  2,  3,  5, 8, 13, 21, 34, 55 }
当 low = 0 时：mid = 0 + 3 - 1 = 2
当 low = 1 时：mid = 1 + 3 - 1 = 3
当 low = 2 时：mid = 2 + 3 - 1 = 4 
当 low = 3 时：mid = 3 + 3 - 1 = 5 , 此时新数组长度为 5，最大下标为 4，已经超过该数组最大个数了，可以认为没有找到。
上面的验证是验证这个公式是否有效，至少不会出现数组越界的情况

那么再来推导验证下改变 k 的值，上面的 k = 4

当 k = 3 ，low = 0 ： mid = 0 + 2 -1 = 1
当 k = 2 ，low = 0 ： mid = 0 + 1 -1 = 0
当 k = 1 ，low = 0 ： mid = 0 + 1 -1 = 0

可以看到移动其中的 k 也是不会导致数组越界的。

那么再来看，k、k-1、k-2 有啥作用

      arr = {1, 8, 10, 1000}  扩充成如下
   newArr = {1, 8, 10, 1000,1000}
   
{1,  1,  2,  3,  5, 8, 13, 21, 34, 55 }
                 ↑
             ↑   k
         ↑  k-1
        k-2
扩充后的数组长度为 5
            - - - - -      这一条线的长度为 5 ，也就是 k = 4
              ↑
 左侧长度为  2         右侧长度为 3 

那么再来看下面的图：

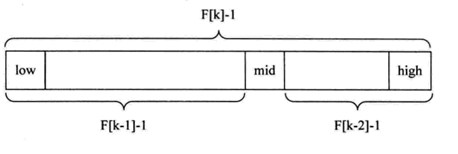
斐波那契数列性质 F[k] = F[k-1] + F[k-2]

由以上性质可以得到上图的组合: F[k]-1 = (F[k -1] -1) + (F[k-2] -1) + 1

上图的公式 F[k - 1] - 1 + 中间 mid 占用 1 个位置 + F[k - 2] -1 + 1 个位置 就是这个数组的所有元素个数。

那么说明：只要顺序表的长度为 F[k]-1，则可以将该表分成 长度为 F[k-1]-1 和 F[k-2]-1 两段，如上图所示

那么中间值则为：mid = low + F[k-1]-1

上面说了这么多，其实也并没有说明白他的这个求中间值的公式为什么是这样，只是得到了最重要的几个信息：

1. 求中间值是通过斐波那契数列来计算的

2. 原始数组和斐波那契数列的关系是：

   1. 原始数组的长度必须扩充至斐波那契数列中某一个值的长度
   2. 因为可以通过斐波那契数列的性质，将这一个扩充数组分成黄金分割的两段
   3. 分成两段后，就可以查找中间值，而这个中间值则可称为黄金分割点
   4. 查找该点，是否是所要查找的值，如果不是，则根据大小，可继续将某一段继续分割，查找他的黄金分割点

3. k：进行 k 的减少或增加，必然可以根据斐波那契数列的特性，将数列分成两段

好了，个人理解差不多就只能这样了，下面看一遍代码实现，你就明白了，只能感叹数学之美。

代码实现

package cn.mrcode.study.dsalgtutorialdemo.datastructure.search;

import org.junit.Test;

import java.util.Arrays;

public class FibonacciSearchTest {
    @Test
    public void fibTest() {
        int[] arr = {1, 8, 10, 89, 1000, 1234};
        System.out.println("原数组：" + Arrays.toString(arr));
        int findVal = 1;
        int result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = -1;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = 8;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = 10;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = 1000;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = 1234;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

        findVal = 12345;
        result = fibSearch(arr, findVal);
        System.out.println("查找值 " + findVal + "：" + (result == -1 ? "未找到" : "找到值，索引为：" + result));

    }

    public static int max_size = 20;

    private int fibSearch(int[] arr, int key) {
        // 构建一个斐波那契数列
        int[] f = fib();
        // 查找 k，由数组长度，找到在斐波那契数列中的一个值
        int k = 0;
        int low = 0;
        int high = arr.length - 1;
        while (high > f[k] - 1) {
            k++;
        }

        // 构建临时数组
        int[] temp = Arrays.copyOf(arr, f[k]);
        // 将临时数组扩充的值用原始数组的最后一个值（最大值）填充
        for (int i = high + 1; i < temp.length; i++) {
            temp[i] = arr[high];
        }

        int mid = 0;
        // 当两边没有交叉的时候，就都可以继续查找
        while (low <= high) {
            if (k == 0) {
                // 如果 k = 0 的话，就只有一个元素了，mid 则就是这个元素
                mid = low;
            } else {
                mid = low + f[k - 1] - 1;
            }
            // 要查找的值说明在数组的左侧
            if (key < temp[mid]) {
                high = mid - 1;
                // 1. 全部元素 = 前面的元素 + 后面的元素
                // 2. f[k] = f[k-1] + f[k-2]
                // k -1 , 得到这一段的个数，然后下一次按照这个个数进行黄金分割
                k--;
            }
            // 要查找的值在数组的右侧
            else if (key > temp[mid]) {
                low = mid + 1;
                k -= 2;
            }
            // 找到的话
            else {
                if (mid <= high) {
                    return mid;
                }
                // 当 mid 值大于最高点的话
                // 也就是我们后面填充的值，其实他的索引就是最后一个值，也就是 high
                else {
                    return high;
                }
            }
        }
        return -1;
    }

    private int[] fib() {
        int[] f = new int[20];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < max_size; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }
}

测试代码输出

原数组：[1, 8, 10, 89, 1000, 1234]
查找值 1：找到值，索引为：0
查找值 -1：未找到
查找值 8：找到值，索引为：1
查找值 10：找到值，索引为：2
查找值 1000：找到值，索引为：4
查找值 1234：找到值，索引为：5
查找值 12345：未找到