# 线索化二叉树
# 引出线索化二叉树
看如下问题:将数列 {1,3,6,8,10,14} 构成一颗二叉树
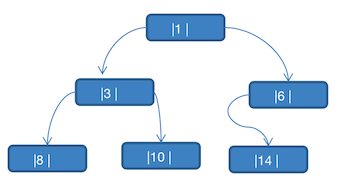
可以看到上图的二叉树为一颗 完全二叉树。对他进行分析,可以发现如下的一些问题:
- 当对上面的二叉树进行中序遍历时,数列为
8,3,10,1,14,6 - 但是
6,8,10,14这几个节点的左右指针,并没有完全用上
如果希望充分利用各个节点的左右指针,让各个节点可以 指向自己的前后节点,这个时候就可以使用 线索化二叉树 了
# 介绍
n 个节点的二叉树链表中含有 n + 1 个空指针域,他的推导公式为 2n-(n-1) = n + 1。
利用二叉链表中的空指针域,存放指向该节点在 某种遍历次序 下的 前驱 和 后继 节点的指针,这种附加的指针称为「线索」
- 前驱:一个节点的前一个节点
- 后继:一个节点的后一个节点
如下图,在中序遍历中,下图的中序遍历为 8,3,10,1,14,6,那么 8 的后继节点就为 3,3 的后继节点是 10
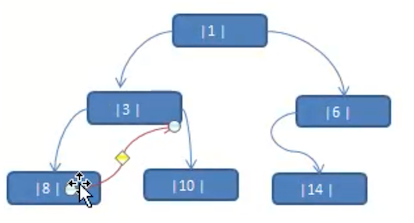
这种加上了线索的二叉树链表称为 线索链表(节点存储了下一个节点,组成了链表,并且一般的二叉树本来就是用链表实现的),相应的二叉树称为 线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为:前、中、后序线索二叉树。
# 思路分析

将上图的二叉树,进行 中序线索二叉树,中序遍历的数列为 8,3,10,1,14,6。
那么以上图为例,线索化二叉树后的样子如下图
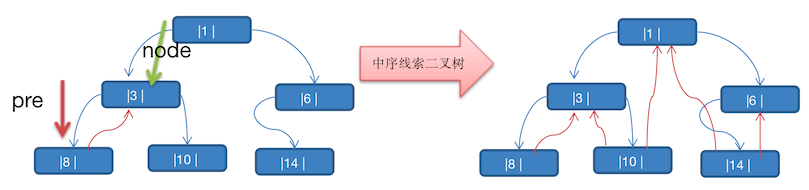
- 8 的后继节点为 3
- 3 由于 左右节点都有元素,不能线索化
- 10 的前驱节点为 3,后继节点为 1
- 1 不能线索化
- 14 的前驱节点为 1,后继节点为 6
- 6 有左节点,不能线索化
注意:当线索化二叉树后,那么一个 Node 节点的 left 和 right 属性,就有如下情况:
left 指向的是 左子树,也可能是指向 前驱节点
例如:节点 1 left 节点指向的是左子树,节点 10 的 left 指向的就是前驱节点
right 指向的是 右子树,也可能是指向 后继节点
例如:节点 3 的 right 指向的是右子树,节点 10 的 right 指向的是后继节点
# 代码实现
下面的代码,有几个地方需要注意:
HeroNode 就是一个 简单的二叉树节点,不同的是多了两个 type 属性:
- leftType:左节点的类型:0:左子树,1:前驱节点
- rightType:右节点的类型:0:右子树,1:后继节点
为什么需要?上面原理讲解了,left 或则 right 会有两种身份,需要一个额外 的属性来指明
threadeNodes:线索化二叉树
是将一颗二叉树,进行线索化标记。只是将可以线索化的节点进行赋值。
package cn.mrcode.study.dsalgtutorialdemo.datastructure.tree;
import org.junit.Test;
/**
* 线索化二叉树
*/
public class ThreadedBinaryTreeTest {
class HeroNode {
public int id;
public String name;
public HeroNode left;
public HeroNode right;
/**
* 左节点的类型:0:左子树,1:前驱节点
*/
public int leftType;
/**
* 右节点的类型:0:右子树,1:后继节点
*/
public int rightType;
public HeroNode(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "HeroNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
class ThreadedBinaryTree {
public HeroNode root;
public HeroNode pre; // 保留上一个节点
/**
* 线索化二叉树:以 中序的方式线索化
*/
public void threadeNodes() {
// 从 root 开始遍历,然后 线索化
this.threadeNodes(root);
}
private void threadeNodes(HeroNode node) {
if (node == null) {
return;
}
// 中序遍历顺序:先左、自己、再右
threadeNodes(node.left);
// 难点就是在这里,如何线索化自己
// 当自己的 left 节点为空,则设置为前驱节点
if (node.left == null) {
node.left = pre;
node.leftType = 1;
}
// 因为要设置后继节点,只有回到自己的后继节点的时候,才能把自己设置为前一个的后继节点
// 当前一个节点的 right 为空时,则需要自己是后继节点
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = 1;
}
// 数列: 1,3,6,8,10,14
// 中序: 8,3,10,1,14,6
// 这里最好结合图示的二叉树来看,容易理解
// 因为中序遍历,先遍历左边,所以 8 是第一个输出的节点
// 当 node = 8 时,pre 还没有被赋值过,则为空。这是正确的,因为 8 就是第一个节点
// 当 8 处理完成之后,处理 3 时
// 当 node = 3 时,pre 被赋值为 8 了。
pre = node;
threadeNodes(node.right);
}
}
@Test
public void threadeNodesTest() {
HeroNode n1 = new HeroNode(1, "宋江");
HeroNode n3 = new HeroNode(3, "无用");
HeroNode n6 = new HeroNode(6, "卢俊");
HeroNode n8 = new HeroNode(8, "林冲2");
HeroNode n10 = new HeroNode(10, "林冲3");
HeroNode n14 = new HeroNode(14, "林冲4");
n1.left = n3;
n1.right = n6;
n3.left = n8;
n3.right = n10;
n6.left= n14;
ThreadedBinaryTree tree = new ThreadedBinaryTree();
tree.root = n1;
tree.threadeNodes();
// 验证:
HeroNode left = n10.left;
HeroNode right = n10.right;
System.out.println("10 号节点的前驱节点:" + left.id);
System.out.println("10 号节点的后继节点:" + right.id);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
测试输出
10 号节点的前驱节点:3
10 号节点的后继节点:1
2
如果看代码注释看不明白的话 ,现在来解释:
线索化的时候,就是要按照 中序遍历 的顺序,去找可以线索化的节点
中序遍历顺序:先左、自己、再右
我们主要的代码是在 自己这一块
确定前一个节点 pre
这个 pre 很难理解,对照下图进行理解

// 数列: 1,3,6,8,10,14 // 中序: 8,3,10,1,14,6 // 因为中序遍历,先遍历左边,所以 8 是第一个输出的节点 // 当 node = 8 时,pre 还没有被赋值过,则为空。这是正确的,因为 8 就是第一个节点 // 当 8 处理完成之后,处理 3 时 // 当 node = 3 时,pre 被赋值为 8 了。1
2
3
4
5
6
7设置前驱节点
难点的讲解在于 pre,这里就简单了
如果当 node = 8 时,pre 还是 null,因为 8 就是中序的第一个节点。因此 8 没有前驱
如果当 node = 3 时,pre = 8,那么 3 是不符合线索化要求的,因为 8 是 3 的 left
设置后继节点
接上面的逻辑。
如果当 node = 8 时,本来 该给 8 设置他的后继节点,但是此时根本就获取不到节点 3,因为节点是单向的。
如果利用前一个节点 pre。
当 node=3 时,pre = 8,这时就可以为节点 8 处理它的后继节点了,因为根据中序的顺序,左、自己、后。那么自己一定是前一个的后继。只要前一个的 right 为 null,就符合线索化
上述最难的 3 个点说明,请对照上图看,先看一遍代码,再看说明。然后去 debug 你就了解了。
# 遍历线索化二叉树
结合图示来看思路说明最直观

对于原来的中序遍历来说,无法使用了,因为左右节点再也不为空了。这里直接利用线索化节点提供的线索,找到他的后继节点遍历,思路如下:
首先找到它的第一个节点,并打印它
中序遍历,先左,所以一直往左找,直到 left 为 null 时,则是第一个节点
然后看它的 right节点是否为线索化节点,是的话则打印它
因为:如果 right 是一个线索化节点,也就是 right 是当前节点的 后继节点,可以直接打印。
right 如果是一个普通节点,那么就直接处理它的右侧节点
因为:按照中序遍历顺序,左、自己、右,这里就理所当然是右了
看描述索然无味,结合下面的代码来看,就比较清楚了
/**
* 遍历线索化二叉树
*/
public void threadedList() {
// 前面线索化使用的是中序,这里也同样要用中序的方式
// 但是不适合使用之前那种递归了
HeroNode node = root;
while (node != null) {
// 中序:左、自己、右
// 数列: 1,3,6,8,10,14
// 中序: 8,3,10,1,14,6
// 那么先找到左边的第一个线索化节点,也就是 8. 对照图示理解,比较容易
while (node.leftType == 0) {
node = node.left;
}
// 找到这个线索化节点之后,打印它
System.out.println(node);
// 如果该节点右子节点也是线索化节点,则打印它
while (node.rightType == 1) {
node = node.right;
System.out.println(node);
}
// 到达这里,就说明遇到的不是一个 线索化节点了
// 而且,按中序的顺序来看:这里应该处理右侧了
node = node.right;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
测试
/**
* 线索化遍历测试
*/
@Test
public void threadedListTest() {
// 1,3,6,8,10,14
HeroNode n1 = new HeroNode(1, "宋江");
HeroNode n3 = new HeroNode(3, "无用");
HeroNode n6 = new HeroNode(6, "卢俊");
HeroNode n8 = new HeroNode(8, "林冲2");
HeroNode n10 = new HeroNode(10, "林冲3");
HeroNode n14 = new HeroNode(14, "林冲4");
n1.left = n3;
n1.right = n6;
n3.left = n8;
n3.right = n10;
n6.left = n14;
ThreadedBinaryTree tree = new ThreadedBinaryTree();
tree.root = n1;
tree.threadeNodes();
tree.threadedList(); // 8,3,10,1,14,6
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
输出信息
HeroNode{id=8, name='林冲2'}
HeroNode{id=3, name='无用'}
HeroNode{id=10, name='林冲3'}
HeroNode{id=1, name='宋江'}
HeroNode{id=14, name='林冲4'}
HeroNode{id=6, name='卢俊'}
2
3
4
5
6
# 前序线索化
public void preOrderThreadeNodes() {
preOrderThreadeNodes(root);
}
/**
* 前序线索化二叉树
*/
public void preOrderThreadeNodes(HeroNode node) {
// 前序:自己、左(递归)、右(递归)
// 数列: 1,3,6,8,10,14
// 前序: 1,3,8,10,6,14
if (node == null) {
return;
}
System.out.println(node);
// 当自己的 left 节点为空,则可以线索化
if (node.left == null) {
node.left = pre;
node.leftType = 1;
}
// 当前一个节点 right 为空,则可以把自己设置为前一个节点的后继节点
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = 1;
}
// 因为是前序,因此 pre 保存的是自己
// 到下一个节点的时候,下一个节点如果是线索化节点 ,才能将自己作为它的前驱节点
pre = node;
// 那么继续往左,查找符合可以线索化的节点
// 因为先处理的自己,如果 left == null,就已经线索化了
// 再往左的时候,就不能直接进入了
// 需要判定,如果不是线索化节点,再进入
// 比如:当前节点 8,前驱 left 被设置为了 3
// 这里节点 8 的 left 就为 1 了,就不能继续递归,否则又回到了节点 3 上
// 导致死循环了。
if (node.leftType == 0) {
preOrderThreadeNodes(node.left);
}
if (node.rightType == 0) {
preOrderThreadeNodes(node.right);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
这里代码相对于中序线索化来说,难点在于:什么时候该继续往左查找,什么时候该继续往右查找。
测试
/**
* 前序线索化
*/
@Test
public void preOrderThreadedNodesTest() {
// 1,3,6,8,10,14
HeroNode n1 = new HeroNode(1, "宋江");
HeroNode n3 = new HeroNode(3, "无用");
HeroNode n6 = new HeroNode(6, "卢俊");
HeroNode n8 = new HeroNode(8, "林冲2");
HeroNode n10 = new HeroNode(10, "林冲3");
HeroNode n14 = new HeroNode(14, "林冲4");
n1.left = n3;
n1.right = n6;
n3.left = n8;
n3.right = n10;
n6.left = n14;
ThreadedBinaryTree tree = new ThreadedBinaryTree();
tree.root = n1;
tree.preOrderThreadeNodes();
// 验证: 前序顺序: 1,3,8,10,6,14
HeroNode left = n10.left;
HeroNode right = n10.right;
System.out.println("10 号节点的前驱节点:" + left.id); // 8
System.out.println("10 号节点的后继节点:" + right.id); // 6
left = n6.left;
right = n6.right;
System.out.println("6 号节点的前驱节点:" + left.id); // 14, 普通节点
System.out.println("6 号节点的后继节点:" + right.id); // 14,线索化节点
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
输出
HeroNode{id=1, name='宋江'}
HeroNode{id=3, name='无用'}
HeroNode{id=8, name='林冲2'}
HeroNode{id=10, name='林冲3'}
HeroNode{id=6, name='卢俊'}
HeroNode{id=14, name='林冲4'}
10 号节点的前驱节点:8
10 号节点的后继节点:6
6 号节点的前驱节点:14
6 号节点的后继节点:14
2
3
4
5
6
7
8
9
10
可以看到,我们线索化二叉树的时候,是按照中序的顺序 1,3,8,10,6,14 的顺序遍历查找处理的。处理之后的 6 号节点两个都是一样的,但是 left 是正常的节点 14,right 是线索化节点 14
# 前序线索化遍历
前序线索化遍历,还是要记住它的特点是:自己、左(递归)、右(递归),那么遍历思路如下:
- 先打印自己
- 再左递归打印
- 直到遇到一个节点有 right 且是后继节点,则直接跳转到该后继节点,继续打印
- 如果遇到的是一个普通节点,则打印该普通节点,完成一轮循环,进入到下一轮,从第 1 步开始
/**
* 前序线索化二叉树遍历
*/
public void preOrderThreadeList() {
HeroNode node = root;
// 最后一个节点无后继节点,就会退出了
// 前序:自己、左(递归)、右(递归)
while (node != null) {
// 先打印自己
System.out.println(node);
while (node.leftType == 0) {
node = node.left;
System.out.println(node);
}
while (node.rightType == 1) {
node = node.right;
System.out.println(node);
}
node = node.right;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
测试代码
@Test
public void preOrderThreadeListTest() {
ThreadedBinaryTree tree = buildTree();
tree.preOrderThreadeNodes();
System.out.println("前序线索化遍历");
tree.preOrderThreadeList(); // 1,3,8,10,6,14
}
2
3
4
5
6
7
测试输出
HeroNode{id=1, name='宋江'}
HeroNode{id=3, name='无用'}
HeroNode{id=8, name='林冲2'}
HeroNode{id=10, name='林冲3'}
HeroNode{id=6, name='卢俊'}
HeroNode{id=14, name='林冲4'}
前序线索化遍历
HeroNode{id=1, name='宋江'}
HeroNode{id=3, name='无用'}
HeroNode{id=8, name='林冲2'}
HeroNode{id=10, name='林冲3'}
HeroNode{id=6, name='卢俊'}
HeroNode{id=14, name='林冲4'}
2
3
4
5
6
7
8
9
10
11
12
13
# 总结
还有一个后序线索化,笔者这里不写了,从前序、中序获取到几个重要的点:
线索化时:
根据不同的「序」,如何进行遍历的同时,处理线索化节点
对于中序来说:
- 先递归到最左节点
- 开始线索化
- 再递归到最右节点
它的顺序:先左(递归)、自己、再右(递归)
对于前序来说:
- 开始线索化
- 一直往左递归
- 一直往右递归
它的顺序:自己、左(递归)、右(递归)
根据不同的「序」,考虑如何跳过或进入下一个节点,因为要考虑前驱和后继
- 中序:由于它的顺序,第一个线索化节点,就是他的顺序的第一个节点,不用管接下来遇到的节点是否已经线索化过了,这是由于它天然的顺序,已经线索化过的节点,不会在下一次处理
- 前序:由于它的顺序,第一个顺序输出的节点,并不是第一个线索化节点。所以它需要对他的 左右节点进行类型判定,是普通节点的话,再按:自己、左、右的顺序进行左、右进行递归,因为下一次出现的节点有可能是已经线索化过的节点,如果不进行判定,就会导致又回到了已经遍历过的节点。就会导致死循环了
遍历线索化时:基本上和线索化时的「序」一致去考虑,何时该进行输出?什么时候遇到后继节点时,跳转到后继节点处理。最重要的一点是:遍历时,不用考虑前驱节点,之用考虑何时通过后继节点进行跳转。