数据结构与算法 系列教程（笔记）

# 完整平衡二叉树（AVL树）

# 二叉排序树可能的问题

一个数列 {1,2,3,4,5,6}，创建一颗二叉排序树（BST）

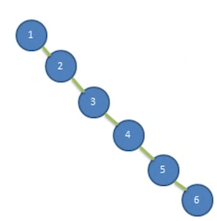
image-20201220170837577

创建完成的树如上图所示，那么它存在的问题有以下几点：

  1. 左子树全部为空，从形式上看，更像一个单链表

  2. 插入速度没有影响

  3. 查询速度明显降低

    因为需要依次比较，不能利用二叉排序树的折半优势。而且每次都还要比较左子树，可能比单链表查询速度还慢。

那么解决这个劣势的方案就是：平衡二叉树（AVL）。

# 基本介绍

平衡二叉树也叫 平衡二叉搜索树（Self-balancing binary search tree），又被称为 AVL 树，可以保证 查询效率较高。它是解决 二叉排序 可能出现的查询问题。

它的特点：是一颗空树或它的 左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一颗平衡二叉树。

平衡二叉树的常用实现方法有：

  • 红黑树
  • AVL（算法）
  • 替罪羊树
  • Treap
  • 伸展树

如下所述，哪些是平衡二叉树？

image-20201220171853831

  1. 是平衡二叉树：

    • 左子树高度为 2
    • 右子树高度为 1

    他们差值为 1

  2. 也是平衡二叉树

  3. 不是平衡二叉树

    1. 左子树高度为 3
    2. 右子树高度为 1

    他们差值为 2，所以不是

# 单旋转（左旋转）

一个数列 4,3,6,5,7,8 ，创建出它对应的平衡二叉树。

思路分析：下图红线部分是调整流程。

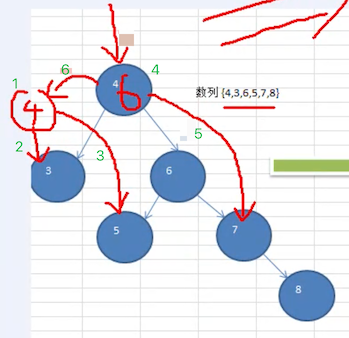
image-20201220190309542

按照规则调整完成之后，形成了下面这样一棵树

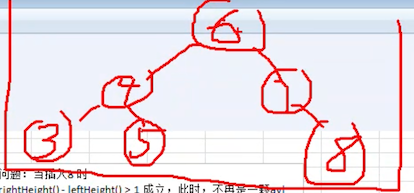
image-20201220190339273

完整流程如下图所示：

image-20201220190245453

插入 8 时，发现左右子树高度相差大于 1，则进行左旋转：

  1. 创建一个新的节点 newNode，值等于当前 根节点 的值（以 4 创建）

  2. 把新节点的 左子树 设置为当前节点的 左子树

    newNode.left = left
    1

  3. 把新节点的 右子树 设置为当前节点的 右子树的左子树

    newNode.right = right.left
    1

  4. 把 当前节点 的值换为 右子节点 的值

    value = right.value
    1

  5. 把 当前节点 的右子树设置为 右子树的右子树

    right = right.right
    1

  6. 把 当前节点 的左子树设置为新节点

    left = newNode
    1

注：左图是调整期，右图是调整后。注意调整期的 6 那个节点，调整之后，没有节点指向他了。也就是说，遍历的时候它是不可达的。那么将会自动的被垃圾回收掉。

# 树高度计算

前面说过，平衡二叉树是为了解决二叉排序树中可能出现的查找效率问题，那么基本上的代码都可以在之前的二叉排序树上进行优化。那么下面只给出与当前主题相关的代码，最后放出一份完整的代码。

树的高度计算，我们需要得到 3 个高度：

  1. 这颗树的整体高度
  2. 左子树的高度
  3. 右子树的高度
public class AvlTreeTest {
    /**
     * 树高度测试
     */
    @Test
    public void heightTest() {
        AvlTree tree = new AvlTree();
        int[] arr = {4, 3, 6, 5, 7, 8};
        for (int i = 0; i < arr.length; i++) {
            tree.add(new Node(arr[i]));
        }
        tree.infixOrder();
        System.out.println("树高度：" + tree.root.height());   // 4
        System.out.println("左树高度：" + tree.root.leftHeight());  // 1
        System.out.println("右树高度：" + tree.root.rightHeight()); // 3
    }
}

/**
 * 排序二叉树
 */
class AvlTree {
    Node root;

    public Node getRoot() {
        return root;
    }
}

/**
 * 节点
 */
class Node {
   /**
     * 以当前节点为基础：计算出它包含它子树的所有高度
     *
     * @return
     */
    public int height() {
        /*
          这里使用了递归：返回了左右子树中，最高的那一个数值。
          递归原理：第一个开始统计的时候，一定是一个叶子节点
                  根据这个逻辑：叶子节点的 Math.max(0,0) = 0
                  因为当前节点算一层，所以 + 1;

                  返回到上一层的时候，至少是这样：Math.max(1,0) = 1
                  然后把自己本身的层 +1。 以此类推，返回到根节点的时候，就拿到了从包含根节点的树的高度
         */
        return Math.max(
                (left == null ? 0 : left.height()),
                (right == null ? 0 : right.height())
        ) + 1;
    }

    /**
     * 计算左子树的高度
     *
     * @return
     */
    public int leftHeight() {
        if (left == null) {
            return 0;
        }
        // 如果从根节点开始的话
        // 其实它从中间分开，左侧就有很多的小树
        // 所以还是要计算左右树的高度，返回一个最大的值，只不过是开始节点变化了
        return left.height();
    }

    /**
     * 计算右子树的高度
     *
     * @return
     */
    public int rightHeight() {
        if (right == null) {
            return 0;
        }
        return right.height();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

测试输出

3
4
5
6
7
8
树高度：4
左树高度：1
右树高度：3
1
2
3
4
5
6
7
8
9

# 旋转

说下旋转的时机：也就是什么时机采取做旋转的操作？

当然是：当 右子树高度 - 左子树高度 > 1 时，才执行左旋转。

这里就得到一些信息:

  1. 每次添加完一个节点后，就需要检查树的高度

  2. 满足 右子树高度 - 左子树高度 > 1，那么一定满足下面的条件：

    1. 左子树高度为 1
    2. 右子树高度为 3

    也就是符合这张图

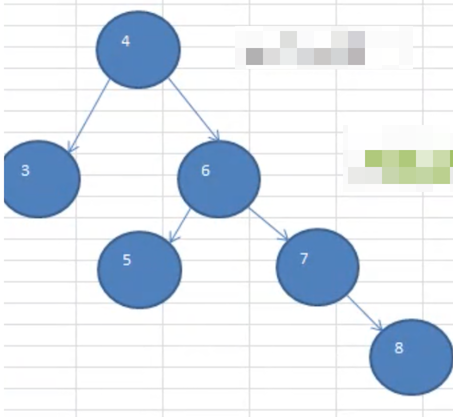
    image-20201220203654437

也正是有如上的信息逻辑，在实现旋转的时候，只要按照思路分析写就可以了，不需要进行边界判定了。

class Node {
      /**
     * 添加节点：按照排序二叉树的要求添加
     *
     * @param node
     */
    public void add(Node node) {
        if (node == null) {
            return;
        }
        // 如果添加的值小于当前节点，则往左走
        if (node.value < value) {
            // 左节点为空，则直接挂在上面
            if (left == null) {
                left = node;
            } else {
                // 否则继续往下查找
                left.add(node);
            }
        } else {
            // 往右走
            if (right == null) {
                right = node;
            } else {
                right.add(node);
            }
        }

        // 旋转的时候有以下规则
        // 每添加一个节点之后：检查树的高度是否平衡
        //      如果右子树高度 - 左子树高度 > 1，则左旋转
        //      也就是说：每次旋转的层只涉及到 4 层(对照笔记上的图示理解)
        if (rightHeight() - leftHeight() > 1) {
            leftRotate();
        }
    }

    /**
     * 以当前节点为根节点，进行左旋转
     */
    public void leftRotate() {
        // 1. 创建一个新的节点 newNode，值等于当前 根节点 的值
        Node newNode = new Node(value);
        // 2. 把 新节点的 左子树 设置为当前节点的左子树
        newNode.left = left;
        // 3. 把 新节点的 右子树 设置为当前节点的 右子树的左子树
        newNode.right = right.left;
        // 4. 把 当前节点的值，替换为 右子树 节点的子
        value = right.value;
        // 5. 把 当前节点 的 右节点 设置为 右子树的右子树
        right = right.right;
        // 6. 把 当前节点 的 左节点 设置为 新节点
        left = newNode;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

测试

    /**
     * 左旋转测试
     */
    @Test
    public void leftRotatedTest() {
        AvlTree tree = new AvlTree();
        int[] arr = {4, 3, 6, 5, 7, 8};
        for (int i = 0; i < arr.length; i++) {
            tree.add(new Node(arr[i]));
        }
        tree.infixOrder();
        System.out.println("树高度：" + tree.root.height());   // 3
        System.out.println("左树高度：" + tree.root.leftHeight());  // 2
        System.out.println("右树高度：" + tree.root.rightHeight()); // 2
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

测试输出

3
4
5
6
7
8
树高度：3
左树高度：2
右树高度：2
1
2
3
4
5
6
7
8
9

看完代码之后，它的旋转其实就是，将 root 节点，往下沉到了，root.right 节点下面。

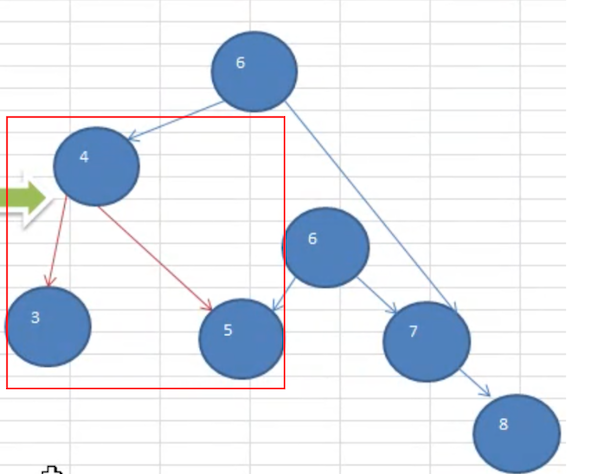
image-20201220203955282

看着上图，是否有想过，貌似根本就可以不用前面讲解的 6 个步骤来旋转：

  1. 不用创建新节点
  2. 直接将 node 节点下沉
  3. 更改 node 的 right 节点为 right.left
  4. 更改 right.left = node

其实就已经完成了旋转。但是你仔细想一想，旋转逻辑是写在 node 里面的， avgTree 中的引用如何改变？除非把旋转逻辑移动到 avgTree 中去，就可以省略掉新建节点的步骤来完成。

# 右旋转

其实这个就很好理解了：

  • 左旋转：右 - 左 > 1，把右边的往左边旋转一层
  • 右旋转：左 - 右 > 1，把左边的往右边旋转一层

他们其实是反着来的，那么右旋转的思路如下：

  1. 创建一个新的节点 newNode，值等于当前 根节点 的值（以 4 创建）

  2. 把新节点的 右子树 设置为当前节点的 右子树

    newNode.right = right
    1

  3. 把新节点的 左子树 设置为当前节点的 左子树的右子树

    newNode.left = left.right
    1

  4. 把 当前节点 的值换为 左子节点 的值

    value = left.value
    1

  5. 把 当前节点 的左子树设置为 左子树的左子树

    left = left.left
    1

  6. 把 当前节点 的右子树设置为新节点

    right = newNode
    1

上述步骤就是对下图的描述：查看图示更清楚

image-20201220205945279

class Node {
  /**
     * 添加节点：按照排序二叉树的要求添加
     *
     * @param node
     */
    public void add(Node node) {
        if (node == null) {
            return;
        }
        // 如果添加的值小于当前节点，则往左走
        if (node.value < value) {
            // 左节点为空，则直接挂在上面
            if (left == null) {
                left = node;
            } else {
                // 否则继续往下查找
                left.add(node);
            }
        } else {
            // 往右走
            if (right == null) {
                right = node;
            } else {
                right.add(node);
            }
        }

        // 旋转的时候有以下规则
        // 每添加一个节点之后：检查树的高度是否平衡
        //      如果右子树高度 - 左子树高度 > 1，则左旋转
        //      也就是说：每次旋转的层只涉及到 4 层(对照笔记上的图示理解)
        if (rightHeight() - leftHeight() > 1) {
            leftRotate();
        }

        if (leftHeight() - rightHeight() > 1) {
            rightRotate();
        }
    }
      /**
     * 以当前节点为根节点，进行右旋转
     */
    public void rightRotate() {
        // 1. 创建一个新的节点 newNode，值等于当前 根节点 的值
        Node newNode = new Node(value);
        // 2. 把 新节点的 右子树 设置为当前节点的右子树
        newNode.right = right;
        // 3. 把 新节点的 左子树 设置为当前节点的 左子树的右子树
        newNode.left = left.right;
        // 4. 把 当前节点的值，替换为 左子树 节点的子
        value = left.value;
        // 5. 把 当前节点 的 左节点 设置为 左子树的左子树
        left = left.left;
        // 6. 把 当前节点 的 右节点 设置为 新节点
        right = newNode;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

测试

    /**
     * 右旋转测试
     */
    @Test
    public void rightRotatedTest() {
        AvlTree tree = new AvlTree();
        int[] arr = {10, 12, 8, 9, 7, 6};
        for (int i = 0; i < arr.length; i++) {
            tree.add(new Node(arr[i]));
        }
        tree.infixOrder();
        System.out.println("树高度：" + tree.root.height());   // 3
        System.out.println("左树高度：" + tree.root.leftHeight());  // 2
        System.out.println("右树高度：" + tree.root.rightHeight()); // 2
        System.out.println("当前根节点：" + tree.root); // 8
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

测试输出

6
7
8
9
10
12
树高度：3
左树高度：2
右树高度：2
当前根节点：Node{value=8}
1
2
3
4
5
6
7
8
9
10

# 双旋转

在前面的例子中，使用单旋转（即一次旋转）就可以将非平衡二叉树转换为平衡二叉树。

但是在某些情况下，就无法做到。比如下面这两组数列

int[] arr ={10,11,7,6,8,9}
int[] arr ={2,1,6,5,7,3}
1
2

运行上面的代码测试可以发现并未生效

    /**
     * 不能通过单旋转解决的场景
     */
    @Test
    public void notLeftOrRightRotatedTest() {
        AvlTree tree = new AvlTree();
        int[] arr = {10, 11, 7, 6, 8, 9};
        for (int i = 0; i < arr.length; i++) {
            tree.add(new Node(arr[i]));
        }
        tree.infixOrder();
        System.out.println("树高度：" + tree.root.height());   // 4
        System.out.println("左树高度：" + tree.root.leftHeight());  // 1
        System.out.println("右树高度：" + tree.root.rightHeight()); // 3
        System.out.println("当前根节点：" + tree.root); // 7
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

测试输出

6
7
8
9
10
11
树高度：4
左树高度：1
右树高度：3
当前根节点：Node{value=7}
1
2
3
4
5
6
7
8
9
10

为什么会出现这种情况呢？看下图

image-20201221215732016

左侧这个树满足 leftHeight - rightHeight > 1 ，也就是满足右旋转，旋转之后，树结构变化了。但是还是一个非平衡二叉树。

它的主要原因是：root 左子树的 左子树高度 小于 右子树的高度。即：节点 7 的左子树高度小于右子树的高度。

解决办法：

  1. 先将 7 这个节点为 root 节点，进行左旋转
  2. 再将原始的 root 节点进行右旋转

过程示意图如下：

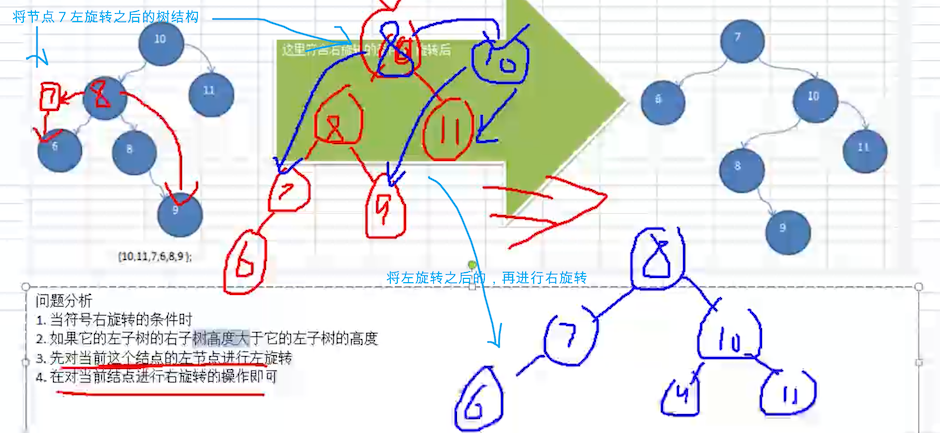
image-20201221222129296

其实可以参考下前面两个单旋转的图例，它有这样一个特点：

  1. 右旋转：

    • root 的 left 左子树高度 大于 右子树高度
    • 右旋转的时候，会将 left.right 旋转到 right.left 节点上

  2. 左旋转：

    • root 的 right 右子树高度 大于 左子树高度
    • 左旋转的时候，会将 right.left 旋转到 left.right 上。

如果不满足这个要求，在第二个操作的时候，就会导致 2 层的高度被旋转到 1 层的节点下面，导致不平衡了。

那么解决代码如下：

在 Node 类的 add 方法中进行双节点逻辑的执行。

    /**
     * 添加节点：按照排序二叉树的要求添加
     *
     * @param node
     */
    public void add(Node node) {
        if (node == null) {
            return;
        }
        // 如果添加的值小于当前节点，则往左走
        if (node.value < value) {
            // 左节点为空，则直接挂在上面
            if (left == null) {
                left = node;
            } else {
                // 否则继续往下查找
                left.add(node);
            }
        } else {
            // 往右走
            if (right == null) {
                right = node;
            } else {
                right.add(node);
            }
        }

        // 旋转的时候有以下规则
        // 每添加一个节点之后：检查树的高度是否平衡
        //      如果右子树高度 - 左子树高度 > 1，则左旋转
        //      也就是说：每次旋转的层只涉及到 4 层(对照笔记上的图示理解)
        // 						  小旋转的时候：只涉及到 3 层，旋转的时候，最多操作了当前节点和左右节点，所以不会导致 NPE 问题
        if (rightHeight() - leftHeight() > 1) {
            // 当 右节点的：左子树高度 大于 右子树的高度时，将 right 节点进行右旋转
            if (right != null && right.leftHeight() > right.rightHeight()) {
                 right.rightRotate();
            }
            leftRotate();
        }

        if (leftHeight() - rightHeight() > 1) {
            // 当 左节点的：右子树高度 大于 左子树的高度时，将 left 节点进行左旋转
            if (left != null && left.rightHeight() > left.leftHeight()) {
                left.leftRotate();
            }
            rightRotate();
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

测试代码

   /**
     * 添加双旋转之后，之前测试不能旋转的数列进行测试
     */
    @Test
    public void doubleRotatedTest() {
        AvlTree tree = new AvlTree();
        int[] arr = {10, 11, 7, 6, 8, 9};
//        int[] arr ={2,1,6,5,7,3}
        for (int i = 0; i < arr.length; i++) {
            tree.add(new Node(arr[i]));
        }
        tree.infixOrder();
        System.out.println("树高度：" + tree.root.height());
        System.out.println("左树高度：" + tree.root.leftHeight());
        System.out.println("右树高度：" + tree.root.rightHeight());
        System.out.println("当前根节点：" + tree.root); 
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

输出信息

6
7
8
9
10
11
树高度：3
左树高度：2
右树高度：2
当前根节点：Node{value=8}


1
2
3
5
6
7
树高度：3
左树高度：2
右树高度：2
当前根节点：Node{value=5}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

← 多路查找树 →