# 二叉树与 B 树
# 二叉树存在的问题
二叉树的操作效率较高,但是也存在问题,如下图所示
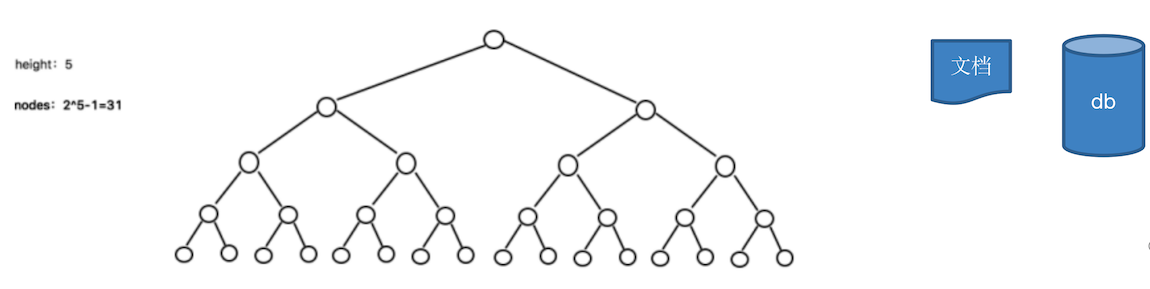
当二叉树的节点较少时,不会出现什么问题。但是当节点过多时(海量,如 1 亿),就会出现如下的问题:
构建二叉树时,需要进行多次 I/O 操作
节点较多时,一般会存储在文件或则数据库中,进行多次 I/O 获取到所有的节点,速度有影响
会造成二叉树的高度很大,降低操作速度
# 多叉树
为了解决层数过多的问题,就出现了 多叉树。
在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是 多叉树(multiway tree)。
多叉树也有一定的规则的,比如后面讲解的 2-3 树、2-3-4 树,就是多叉树。
多叉树通过重新组织节点,减少树的高度,对二叉树进行优化。
下图则是一颗 2-3 的多叉树:
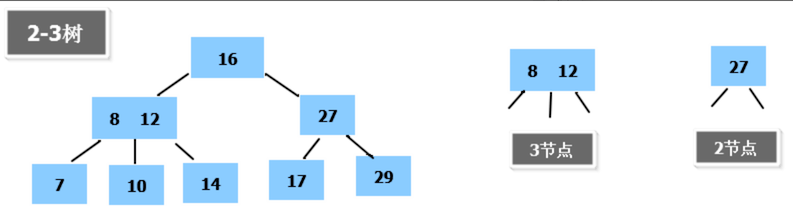
2-3 的原因:如上图按节点数量来定义的。有的只有 2 个子节点,有的有 3 个子节点。
# B 树的基本介绍
B 树通过重新组织节点,降低树的高度,并且减少 I/O 读写次数来提升效率。

上图说明:
- 一个圆圈表示一个数据项
- 相连的数据项,整个表示一个节点
那么它的有点如何理解呢?
降低树的高度:
可以看到,一个节点中有很多数据项,就能大大减少节点数量,从而降低树的高度
减少 I/O 读写次数
文件系统及数据库系统的设计者利用了 磁盘预读原理,将一个节点的大小设为等于一个页(通常大小为 4K),这样每个节点只需要一次 I/O 就可以完全载入。
这样说,你可能没有概念,举个例子:将树的度 M 设置为 1024 ,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素。
B 树(B+ )广泛应用于文件存储系统以及数据库系统中。
什么是 度?
- 节点的度:一个节点下的子树节点个数就是 节点的度。
- 树的度:指一颗树中,节点的度最大的哪一个值。
B 树其实就是前面所说的 多叉树