# 树
# 2-3 树
2-3 树是最简单的 B 树结构,具有如下特点:
所有 叶子节点 都在同一层
只要是 B 树都满足这个条件,就是满树。
有两个子节点的节点叫 二节点
二节点要么 没有子节点,要么 必须有两个子节点。
有三个子节点的节点叫 三节点
三节点要么 没有子节点,要么 必须有三个子节点。
2-3 树是由 二节点 和 三节点 构成的树
# 2-3 树构建图解
对数列 {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成一个 2-3 树,那么它构建的规则要满足前面说的特点。下面进行图解后,你就明白,上面的特点是如何限制的。
有几个额外的注意事项:
- 一个节点中,最多只允许放 2 个数据。
- 构建的树必须是有序的,也就是按照二叉排序(BST)的要求构建有序的树
下面是图解步骤:
添加 16、24
添加 16 时,没有数据,直接新建一个节点,放进去。
添加 24 时,发现有一个节点了,并且比 16 大,此时该节点中只有一个数据,则将 24 放在 16 的右边。
添加 12
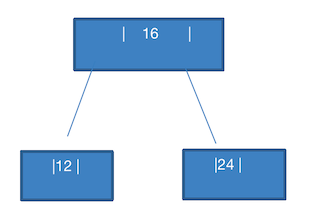
此时会发现,12 比 16 小,本来应该放在 16 的左边,此时发现这个节点 已经有两个数据了,那么就只能放在 左子节点 。
如果直接将 12 放到
16,24的左节点,就会破坏 2-3 树的条件:2 节点,要么没有子节点,要么有两个。那么此时就只能将
16,24这个节点进行拆分。如上图:24 变成 16 的右节点,12 变成 16 的左节点。这时就满足了 2-3 的特性。添加 32
这个就简单了,以现在的树结构,可以直接添加到 24 的 右边,变成
24,32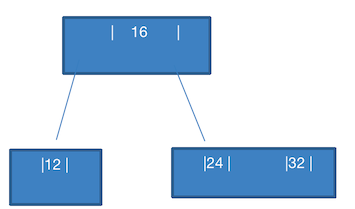
添加 14
这个也简单,直接添加到 12 的右边,变成
12,14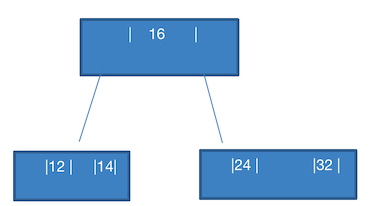
添加 26
此时应该添加到
24,32的中间,由于一个节点只能添加两个数据,那么就需要拆分。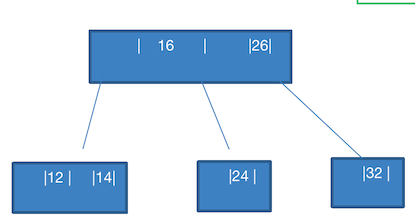
为了满足 B 树特点,发现上层的
16只有一个数,那么就补足它。组成16,26。因为此时
24,32这个节点,不满足 BST 的排序了,24 是小于 26 的。只有 32 满足。拆完上层,再拆本层:由于 24 介于
16,26之间,则将它安排在 3 节点中的中间节点,24,32把 24 拆分出去了,只剩下32,此时完全满足 B 树的特点。添加 34
此时就简单了,添加到
32,34中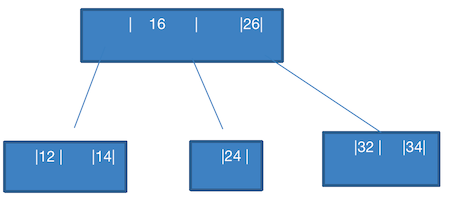
添加 10
此时应该添加到
12,14的左侧。但是不满足条件:一个节点最多只能装 2 个数据。放到
12,14的左节点,也不满足条件:所有叶子节点必须在同一层、也不满足 2-3 节点的数量要求。那么此时就需要拆分,先看他的上层
16,26是满的,如何做呢?看下图: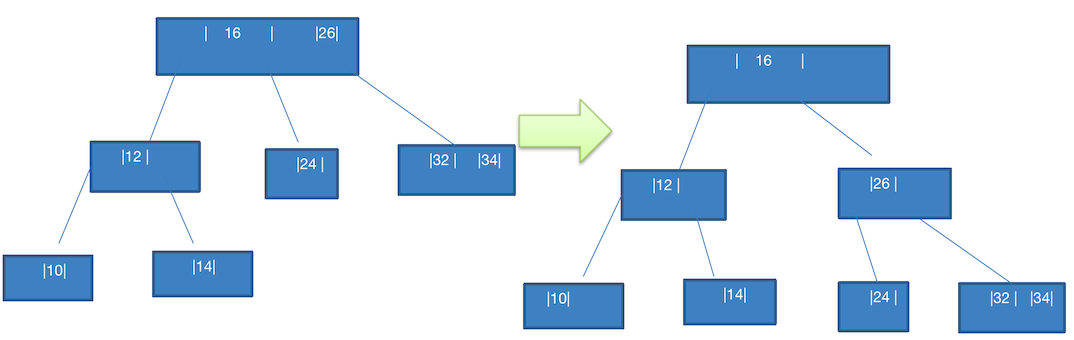
左侧的拆分图,上面我们分析过了,不满足 B 树要求。那么就需要拆分成右图这样:
- 将
12,14中的 14 拆分成 右子节点,10 挂在 左节点。 - 此时不满足 B 树要求的,则将
16,26中的 26 拆分成 右子节点。 24这个节点由于上层被拆分了,不满足在中间节点了。调整它的位置- 原来的
32,34节点调整为16的右节点。
- 将
添加 8
此时很简单,组成
8,10即可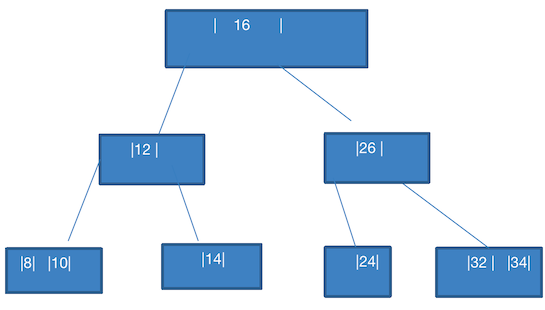
添加 28
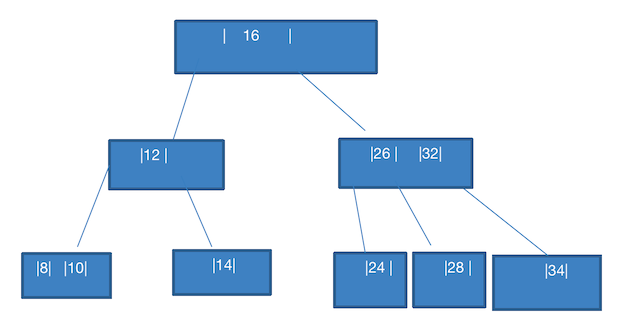
这里笔者有点小小的疑问,此时 28 不是应该加在
26,28吗?难道说这里还有一个规则:- 只有一个数据的节点,下面只允许 最多有 2 个节点,要么没有
- 有 2 个数据的节点,下面只允许 最多有 3 个节点,要么没有
添加 38
此时就简单,直接组成 34,38
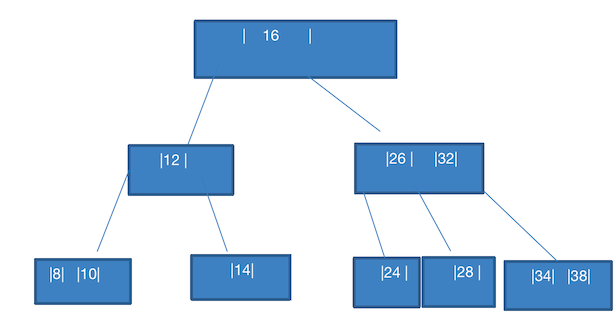
添加 20
这个也简单,直接组成
20,24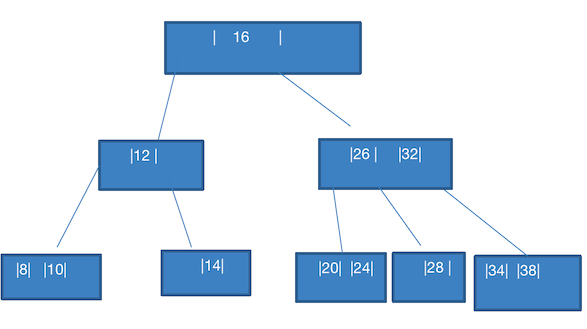
# 2-3 树添加规则总结
满足如下特点:
所有 叶子节点 都在同一层
只要是 B 树都满足这个条件,就是满树。
有两个子节点的节点叫 二节点
二节点要么 没有子节点,要么 必须有两个子节点。
有三个子节点的节点叫 三节点
三节点要么 没有子节点,要么 必须有三个子节点。
2-3 树是由 二节点 和 三节点 构成的树
构建的树,要满足二叉排序树(BST) 的顺序
一个节点中,最多只允许放 2 个数据。
只有一个数据的节点,下面只允许 最多有 2 个节点,要么没有
有 2 个数据的节点,下面只允许 最多有 3 个节点,要么没有
# 234 树
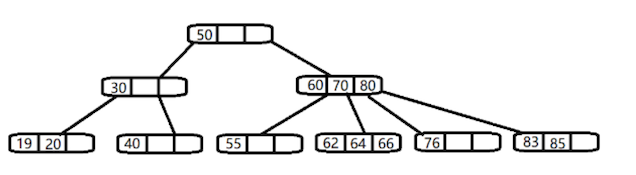
除了 2-3 树,还有 2-3-4 树,他的特点是在 2-3 树的基础上,还多了一个 4 节点,同样,一个节点最多可以装 3 个数据,要么有 4 个节点,要么没有
← 二叉树与 B 树 B 树、B+ 树、B*树 →