# 广度优先算法的代码实现
记住这个步骤:
- 访问初始节点 v ,并标记节点 v 为已访问
- 节点 v 入队列
- 当队列非空时,继续执行,否则算法结束(仅对 v 的节点算法结束)。
- 出队列,取得队头的节点 u
- 查找节点 u 的第一个邻接节点 w
- 若节点 u 的邻接节点 w 不存在,则跳转到步骤 3;否则执行以下三个步骤:
- 若节点 w 尚未被访问,则访问节点 w 并标记为已访问
- 节点 w 入队列
- 查找节点 u 的继 w 邻接节点后的下一个邻接节点 w,转到步骤 6
下面的代码实现也是这个步骤来实现的
/**
* 对整个节点进行 广度优先 遍历
*/
public void bsf() {
for (int i = 0; i < vertexs.size(); i++) {
// 如果已经访问过,则跳过
if (isVisiteds[i]) {
continue;
}
System.out.println("新的节点广度优先"); // 换行 1
// 没有访问过,则以此节点为基础进行深度遍历
bsf(i);
}
}
/**
* 对单个节点为初始节点,进行广度优先遍历
*
* @param i
*/
private void bsf(int i) {
// 访问该节点,并标记已经访问
System.out.print(getValueByIndex(i) + " → ");
isVisiteds[i] = true;
// 将访问过的添加到队列中
LinkedList<Integer> queue = new LinkedList<>();
queue.addLast(i); // 添加到末尾
int u; // 队列头的节点
int w; // u 的下一个邻接节点
// 当队列不为空的时候,查找节点 u 的第一个邻接节点 w
while (!queue.isEmpty()) {
// System.out.println(); // 换行 2
u = queue.removeFirst();
w = getFirstNeighbor(u);
// w 存在的话
// while (w != -1) {
// // 如果 w 已经被访问过
// if (isVisiteds[w]) {
// // 则:以 u 为初始节点,查找 w 的下一个邻接节点
// w = getNextNeighbor(u, w);
// }
// // 如果 w 没有被访问过,则访问它,并标记已经访问
// else {
// System.out.print(getValueByIndex(w) + " → ");
// isVisiteds[w] = true;
// queue.addLast(w); // 访问过的一定要入队列
// }
// }
// 上面这样写,容易阅读,但是会存在多一次循环的问题,改写成下面这样
while (w != -1) {
// 如果没有被访问过,则访问,并标记为已经访问过
if (!isVisiteds[w]) {
System.out.print(getValueByIndex(w) + " → ");
isVisiteds[w] = true;
queue.addLast(w); // 访问过的一定要入队列
}
// 上面访问之后,就需要获取该节点的下一个节点
// 否则,下一次还会判断一次 w,然后去获取下一个节点,只获取,但是没有进行访问相关操作
// 相当于每个节点都会循环两次,这里减少到一次
w = getNextNeighbor(u, w);
}
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
测试代码
/**
* 图的广度优先遍历
*/
@Test
public void bfsTest() {
int n = 5;
String vertexValue[] = {"A", "B", "C", "D", "E"};
Grap grap = new Grap(n);
for (String value : vertexValue) {
grap.insertVertex(value);
}
// a,b a,c b,c b,d b,e
grap.insertEdge(0, 1, 1);
grap.insertEdge(0, 2, 1);
grap.insertEdge(1, 2, 1);
grap.insertEdge(1, 3, 1);
grap.insertEdge(1, 4, 1);
grap.showGraph();
System.out.println();
grap.bsf();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
测试输出
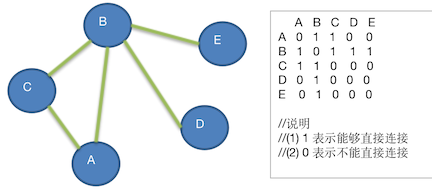
A B C D E
A 0 1 1 0 0
B 1 0 1 1 1
C 1 1 0 0 0
D 0 1 0 0 0
E 0 1 0 0 0
A → B → C → D → E →
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
当只打开 换行 1 的时候,输出如下信息
System.out.println("新的节点广度优先"); // 换行 1
A → B → C → D → E →
1
2
2
然后同时打开 换行 1、2,输出信息如下
新的节点广度优先
A →
B → C →
D → E →
1
2
3
4
5
6
7
2
3
4
5
6
7
可以看到:
- 先输出了 A:因为 A 是初始节点
- 然后以 A 为基础,找与 A 直连的,B、C,由于后面没有了,则会退出一个小循环
- 然后从队列中取出头:也就是 B,因为前面记录了访问顺序,找与 B 直连的,进入小循环
- 输出了与 B 直连的:D、E
通过这个过程可以看到:广度优先,他是一层一层的查找的。