# 普利姆算法
# 应用场景-修路问题
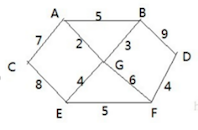
胜利乡有 7 个村庄(A, B, C, D, E, F, G) ,现在需要修路把 7 个村庄连通,各个 村庄的距离用边线表示(权) ,比如 A – B 距离 5 公里
问:如何修路保证各个村庄都能连通,并且总的修建公路 总里程最短?
思路:
只满足连通:将 10 条边,连接即可,但是总的里程数不是最小.
满足连通,又保证总里程最短:就是尽可能的选择少的路线,并且每条路线最小,保证总里程数最少
# 最小生成树
修路问题本质就是就是 最小生成树问题, 最小生成树(Minimum Cost Spanning Tree),简称 MST。
给定一个 带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树 ,它有如下特点:
- N 个顶点,一定有
N-1条边 - 包含全部顶点
N-1条边都在图中
比如下图:
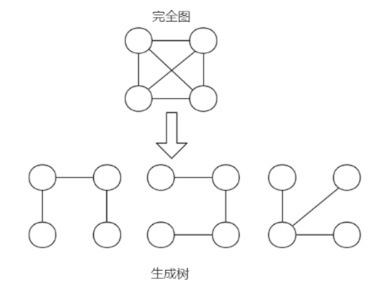
求最小生成树的算法主要是 普里姆 算法 和 克鲁斯卡尔算法
# 普利姆算法介绍
普利姆(Prim)算法求最小生成树,也就是:在包含 n 个顶点的连通图中,找出只有(n-1)条边包含所有 n 个顶点的连通子图,也就是所谓的 极小连通子图
它的算法如下:
- 设
G=(V,E)是连通网T=(U,D)是最小生成树V、U 是顶点集合
E、D 是边的集合
若从顶点 u 开始构造最小生成树,则从集合 V 中取出顶点 u 放入集合 U 中,标记顶点 v 的
visited[u]=1若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边,则寻找这些边中权值最小的边,但不能构成回路,将顶点 vj 加入集合U中,将边(ui,vj)加入集合 D 中,标记
visited[vj]=1重复步骤 ②,直到 U 与 V 相等,即所有顶点都被标记为访问过,此时 D 中有 n-1 条边
# 普利姆算法图解
以这个为例子:

从 A 点开始处理
与 A 直连的点有:
A,C [7]:后面中括号中的是他的权值A,B [5]A,G [2]
在这个所有的边中,
A,G [2]的权值最小,那么结果是:A、G从
A、G开始,找到他们的直连边,但是不包含已经访选择过的边。A,C [7]A,B [5]G,B [3]G,E [4]G,F [6]
在以上边中,权值最小的是:
G,B [3],那么结果是:A、G、B以
A、G、B开始,找到他们的直连边,但是不包含已经访选择过的边。A,C [7]A,B [5]G,E [4]G,F [6]B,D [9]
在以上边中,权值最小的是:
G,E [4],那么结果是:A、G、B、EA、G、B、E→ 权值最小的边是E,F [5]→A、G、B、E、FA、G、B、E、F→ 权值最小的边是F,D [4]→A、G、B、E、F、DA、G、B、E、F、D→ 权值最小的边是A,C [7]→A、G、B、E、F、D、C
那么最终结果则为下图:
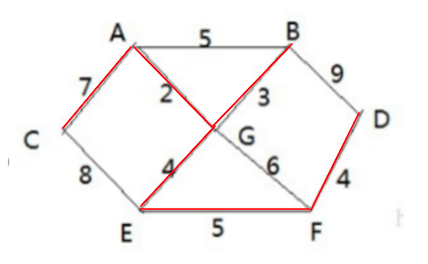
总里程数量为:2+3+4+5+4+7=25
# 代码实现
# 生成图
package cn.mrcode.study.dsalgtutorialdemo.algorithm.prim;
import org.junit.Test;
/**
* 普利姆算法
*/
public class PrimAlgorithm {
/**
* 图:首先需要有一个带权的连通无向图
*/
class MGraph {
int vertex; // 顶点个数
int[][] weights; // 邻接矩阵
char[] datas; // 村庄数据
/**
* @param vertex 村庄数量, 会按照数量,按顺序生成村庄,如 A、B、C...
* @param weights 需要你自己定义好那些点是连通的,那些不是连通的
*/
public MGraph(int vertex, int[][] weights) {
this.vertex = vertex;
this.weights = weights;
this.datas = new char[vertex];
for (int i = 0; i < vertex; i++) {
// 大写字母 A 从 65 开始
datas[i] = (char) (65 + i);
}
}
public void show() {
System.out.printf("%-8s"," ");
for (char vertex : datas) {
// 控制字符串输出长度:少于 8 位的,右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", datas[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
}
@Test
public void mGraphTest() {
// 不连通的默认值:
// 这里设置为较大的数,是为了后续的计算方便,计算权值的时候,不会选择
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
测试输出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
2
3
4
5
6
7
8
使用邻接矩阵构建了一个无向图,按照题目中的连通要求进行构建。

# 最小生成树
/**
* 最小生成树
*/
class MinTree {
/**
* 普利姆算法
*
* @param mGraph 无向图
* @param v 从哪一个点开始生成
*/
public void prim(MGraph mGraph, int v) {
int minTotalWeight = 0; // 记录已选择的边的总权值,仅仅只是为了测试打印验证
// 记录已经选择过的节点
boolean[] selects = new boolean[mGraph.vertex];
// 从哪个节点开始,则标识已经被访问
selects[v] = true;
// 一共要生成 n-1 条边
for (int i = 1; i < mGraph.vertex; i++) {
// 每次循环:选择一条权值最小的边出来
// 记录最小值
int minWeight = 10000;
int x = -1;
int y = -1;
// 每次查找权值最小的边:根据思路,每次都是从已经选择过的点,中去找与该点直连的点的权值
// 并且该点还没有被选择过:如果两个点都被选择过,要么他们是双向的,要么就是被其他的点选择过了
// 这里双循环的含义:建议对照笔记中步骤分析理解
for (int j = 0; j < mGraph.vertex; j++) {
for (int k = 0; k < mGraph.vertex; k++) {
// 通过 j 来限定已经选择过的点
// 通过 k 来遍历匹配,没有选择过的点
// 假设第一轮是 A 点:j = 0
// 那么在这里将会执行 0,1 0,2, 0,3 也就是与 A 点直连,且没有被选择过的点,的最小权值
if (selects[j] && !selects[k]
&& mGraph.weights[j][k] < minWeight
) {
// 记录最小权值,与这条边的信息
minWeight = mGraph.weights[j][k];
x = j;
y = k;
}
}
}
// 当一次循环结束时:就找到了一条权值最小的边
System.out.printf("%s,%s [%s] \n", mGraph.datas[x], mGraph.datas[y], mGraph.weights[x][y]);
minTotalWeight += mGraph.weights[x][y]; // 统计已选择边权值
minWeight = 10000;
// 记录该点已经被选择
// 在查找最小权值边的代码中:y=k, k 表示没有被选择过的点,所以,找到之后,这里记录 y 为这条边的另一个点
selects[y] = true;
}
System.out.println("总权值:" + minTotalWeight);
}
}
@Test
public void primTest() {
// 不连通的默认值:
// 这里设置为较大的数,是为了后续的计算方便,计算权值的时候,不会选择
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
MinTree minTree = new MinTree();
minTree.prim(mGraph, 0);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
测试输出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
A,G [2]
G,B [3]
G,E [4]
E,F [5]
F,D [4]
A,C [7]
总权值:25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
测试结果也就是这个图

下面看看起始点不同的输出信息,从 B 点开始:minTree.prim(mGraph, 1);
B,G [3]
G,A [2]
G,E [4]
E,F [5]
F,D [4]
A,C [7]
总权值:25
2
3
4
5
6
7
可以看到:顺序不同,但是边和总权值是相同的。