# 马踏棋盘算法

# 马踏棋盘游戏介绍

马踏棋盘算法也被称为 骑士周游问题

将马随机放在国际象棋的 8×8 棋盘Board [0～7][0～7] 的某个方格中，马按走棋规则(马走日字)进行移动。要求每个方格只进入一次，走遍棋盘上全部 64 个方格

这个是一个在线游戏，可以去体验下 (opens new window)

如下图所示：马可以走的格子为下图有红色数字的格子

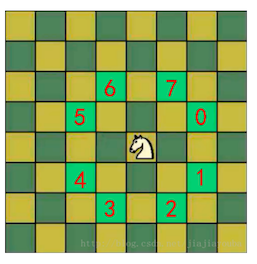
# 思路分析

马踏棋盘问题(骑士周游问题)实际上是 图的深度优先搜索(DFS)的应用。

如果使用回溯（就是深度优先搜索）来解决，假如马儿踏了 53 个点，如图：走到了第 53 个，坐标 （1,0），发现已经走到尽头，没办法，那就只能回退了，查看其他的路径，就在棋盘上不停的回溯

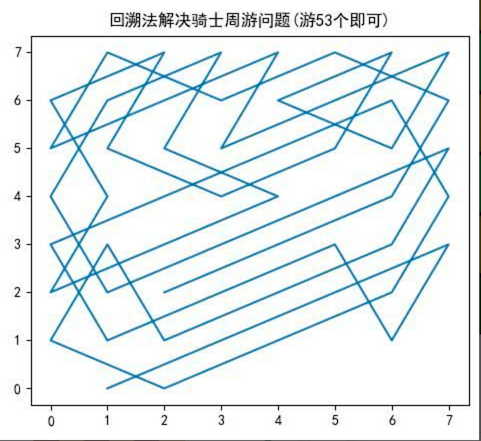
解决步骤：

创建棋盘 chessBoard ，用一个二维数组表示
将当前位置设置为已访问，且每走一步，通过计数器 step+1

并且存入棋盘中，表示那一个格子是走的第几步。因为步序不同，能完成的方式也不同
然后根据当前位置计算马儿可以走的位置

比如上图马儿可以走的位置有 8 个
遍历获取到马儿可以走的位置列表

如果该位置没有走过，则访问它（递归，从第 2 步开始）

如果已经走过则放弃该点
判断马儿是否完成了任务

可以通过 setp 与棋盘大小判定，比如 8x8=64，setp >= 64 则完成了任务。

如果马儿没有完成任务，则需要进行重置当前访问的这个点为没有访问过，因为在回缩的时候，有可能其他的走法能走该点

# 代码实现

由于 根据当前位置计算马儿可以走的位置 这个方法是个独立且有点代码量的函数，我们先完成它

# 根据当前位置计算马儿可以走的位置

如何计算，看下面的图示，你就明白如何实现了

马儿的坐标为 4,4:

获取第 0 个点公式为：4-1,4+2 → x-1,y+2
获取第 1 个点公式为：4+1,4+2→ x+1,y+2
获取第 2 个点公式为：4+2,4-1 → x+2,y-1
获取第 3 个点公式为：4+2,4+1→ x+2,y+1
获取第 4 个点公式为：4+1,4-2 → x+1,y-2
获取第 5 个点公式为：4-1,4-2→ x-1,y-2
获取第 6 个点公式为：4-2,4-1 → x-2,y-1
获取第 7 个点公式为：4-2,4+1→ x-2,y+1

package cn.mrcode.study.dsalgtutorialdemo.algorithm.horse;

import org.junit.Test;

import java.awt.*;
import java.util.ArrayList;


/**
 * 骑士周游问题-马踏棋盘算法
 */
public class HorseChessboard {
    @Test
    public void nextTest() {
        // 测试
        Point current = new Point(4, 4);
        System.out.println(current + " 下一步可选位置有：");
        ArrayList<Point> next = next(current);
        System.out.println(next);

        // 测试一个 0,0
        current = new Point(0, 0);
        System.out.println(current + " 下一步可选位置有：");
        next = next(current);
        System.out.println(next);
    }

    int X = 8; // 棋盘的行数
    int Y = 8; // 棋盘的列数

    /**
     * 根据马儿所在的位置，查找它下一步可以走的位置
     *
     * @param current
     * @return
     */
    public ArrayList<Point> next(Point current) {
        ArrayList<Point> result = new ArrayList<>();
        int cx = current.x;
        int cy = current.y;
        // 第 0 个点
        if (cx - 1 >= 0 && cy + 2 < Y) {
            result.add(new Point(cx - 1, cy + 2));
        }
        // 第 1 个点
        if (cx + 1 < X && cy + 2 < Y) {
            result.add(new Point(cx + 1, cy + 2));
        }
        // 第 2 个点
        if (cx + 2 < X && cy - 1 >= 0) {
            result.add(new Point(cx + 2, cy - 1));
        }
        // 第 3 个点
        if (cx + 2 < X && cy + 1 < Y) {
            result.add(new Point(cx + 2, cy + 1));
        }
        // 第 4 个点
        if (cx + 1 < X && cy - 2 >= 0) {
            result.add(new Point(cx + 1, cy - 2));
        }
        // 第 5 个点
        if (cx - 1 >= 0 && cy - 2 >= 0) {
            result.add(new Point(cx - 1, cy - 2));
        }
        // 第 6 个点
        if (cx - 2 >= 0 && cy - 1 >= 0) {
            result.add(new Point(cx - 2, cy - 1));
        }
        // 第 7 个点
        if (cx - 2 >= 0 && cy + 1 < Y) {
            result.add(new Point(cx - 2, cy + 1));
        }
        return result;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

测试输出

java.awt.Point[x=4,y=4] 下一步可选位置有：
[java.awt.Point[x=3,y=6], java.awt.Point[x=5,y=6], java.awt.Point[x=6,y=3], java.awt.Point[x=6,y=5], java.awt.Point[x=5,y=2], java.awt.Point[x=3,y=2], java.awt.Point[x=2,y=3], java.awt.Point[x=2,y=5]]
java.awt.Point[x=0,y=0] 下一步可选位置有：
[java.awt.Point[x=1,y=2], java.awt.Point[x=2,y=1]]

1
2
3
4

对照下图的坐标检查下，完全正确

下面来写马踏棋盘算法的深度遍历 + 回溯核心代码

# 马踏棋盘算法核心代码

package cn.mrcode.study.dsalgtutorialdemo.algorithm.horse;

import org.junit.Test;

import java.awt.*;
import java.time.Duration;
import java.time.Instant;
import java.util.ArrayList;
import java.util.Arrays;


/**
 * 骑士周游问题-马踏棋盘算法
 */
public class HorseChessboard {
    @Test
    public void nextTest() {
        // 测试
        Point current = new Point(4, 4);
        System.out.println(current + " 下一步可选位置有：");
        ArrayList<Point> next = next(current);
        System.out.println(next);

        // 测试一个 0,0
        current = new Point(0, 0);
        System.out.println(current + " 下一步可选位置有：");
        next = next(current);
        System.out.println(next);
    }

    int X = 8; // 棋盘的行数
    int Y = 8; // 棋盘的列数

    /**
     * 根据马儿所在的位置，查找它下一步可以走的位置; 从 0 ~ 7 的策略，耗时很长很长，回溯太久了，好几分钟都出不来
     *
     * @param current
     * @return
     */
    public ArrayList<Point> next1(Point current) {
        ArrayList<Point> result = new ArrayList<>();
        int cx = current.x;
        int cy = current.y;
        // 第 0 个点
        if (cx - 1 >= 0 && cy + 2 < Y) {
            result.add(new Point(cx - 1, cy + 2));
        }
        // 第 1 个点
        if (cx + 1 < X && cy + 2 < Y) {
            result.add(new Point(cx + 1, cy + 2));
        }
        // 第 2 个点
        if (cx + 2 < X && cy - 1 >= 0) {
            result.add(new Point(cx + 2, cy - 1));
        }
        // 第 3 个点
        if (cx + 2 < X && cy + 1 < Y) {
            result.add(new Point(cx + 2, cy + 1));
        }
        // 第 4 个点
        if (cx + 1 < X && cy - 2 >= 0) {
            result.add(new Point(cx + 1, cy - 2));
        }
        // 第 5 个点
        if (cx - 1 >= 0 && cy - 2 >= 0) {
            result.add(new Point(cx - 1, cy - 2));
        }
        // 第 6 个点
        if (cx - 2 >= 0 && cy - 1 >= 0) {
            result.add(new Point(cx - 2, cy - 1));
        }
        // 第 7 个点
        if (cx - 2 >= 0 && cy + 1 < Y) {
            result.add(new Point(cx - 2, cy + 1));
        }
        return result;
    }

    /**
     * 从 5 ~ 7，7 ~ 0 ，这个策略大概需要 44 秒
     * @param current
     * @return
     */
    public ArrayList<Point> next(Point current) {
        ArrayList<Point> result = new ArrayList<>();
        int cx = current.x;
        int cy = current.y;
        // 第 5 个点
        if (cx - 1 >= 0 && cy - 2 >= 0) {
            result.add(new Point(cx - 1, cy - 2));
        }
        // 第 6 个点
        if (cx - 2 >= 0 && cy - 1 >= 0) {
            result.add(new Point(cx - 2, cy - 1));
        }
        // 第 7 个点
        if (cx - 2 >= 0 && cy + 1 < Y) {
            result.add(new Point(cx - 2, cy + 1));
        }
        // 第 0 个点
        if (cx - 1 >= 0 && cy + 2 < Y) {
            result.add(new Point(cx - 1, cy + 2));
        }
        // 第 1 个点
        if (cx + 1 < X && cy + 2 < Y) {
            result.add(new Point(cx + 1, cy + 2));
        }
        // 第 2 个点
        if (cx + 2 < X && cy - 1 >= 0) {
            result.add(new Point(cx + 2, cy - 1));
        }
        // 第 3 个点
        if (cx + 2 < X && cy + 1 < Y) {
            result.add(new Point(cx + 2, cy + 1));
        }
        // 第 4 个点
        if (cx + 1 < X && cy - 2 >= 0) {
            result.add(new Point(cx + 1, cy - 2));
        }
        return result;
    }

    private boolean finished; // 是否已经完成，由于是递归，在某一步已经完成，回溯时就可以跳过
    private boolean[] visited = new boolean[X * Y];  // 标记是否访问过，访问过的不再访问

    /**
     * 马踏棋盘算法核心代码
     *
     * @param chessboard 棋盘，用于标识哪一个点是第几步走的
     * @param cx         当前要尝试访问的点 x 坐标（行）
     * @param cy         当前要尝试访问的点 y 坐标（列）
     * @param step       当前是第几步
     */
    public void traversalChessboard(int[][] chessboard, int cx, int cy, int step) {
        // 1. 标识当前点已经访问
        visited[buildVisitedIndex(cx, cy)] = true;
        // 2. 标识当前棋盘上的点是第几步走的
        chessboard[cx][cy] = step;
        // 3. 根据当前节点计算马儿可以走的点
        ArrayList<Point> points = next(new Point(cx, cy));
        //  不为空则可以一直尝试走
        while (!points.isEmpty()) {
            Point point = points.remove(0);
            // 如果该点，没有被访问过，则递归访问：深度优先
            if (!visited[buildVisitedIndex(point.x, point.y)]) {
                traversalChessboard(chessboard, point.x, point.y, step + 1);
            }
        }

        // 所有可走的点都走完了，如果还没有完成，则重置当前访问的点为没有访问过

        if (step < X * Y && !finished) {
            visited[buildVisitedIndex(cx, cy)] = false;
            chessboard[cx][cy] = 0; // 重置为 0 表示没有走过
        } else {
            finished = true;  // 表示已经完成任务
        }
//        System.out.println(step);
//        show(chessboard);
    }

    /**
     * 使用的是一个一维数组来表示某个点是否被访问过
     * <pre>
     *   那么就直接数格子，第 N 个格子对应某一个点，从左到右，上到下数
     *   0,1,2,3,4,5,6,7,
     *   8,9,10,11...
     * </pre>
     *
     * @param cx
     * @param xy
     * @return
     */
    private int buildVisitedIndex(int cx, int xy) {
        //比如 0,1: 0*8 + 1 =  1
        return cx * X + xy;
    }

    @Test
    public void traversalChessboardTest() {
        int[][] chessboard = new int[X][Y];
        Instant start = Instant.now();
        traversalChessboard(chessboard, 0, 0, 1);
        Duration re = Duration.between(start, Instant.now());
        System.out.println("耗时：" + re.toMillis() + "毫秒");
        System.out.println("耗时：" + re.getSeconds() + "秒");
        show(chessboard);
    }

    private void show(int[][] chessboard) {
        for (int[] row : chessboard) {
            System.out.println(Arrays.toString(row));
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196

测试输出

耗时：45119毫秒
耗时：45秒
[1, 16, 13, 8, 3, 20, 33, 10]
[26, 7, 2, 15, 12, 9, 4, 21]
[17, 14, 27, 6, 19, 32, 11, 34]
[58, 25, 18, 31, 28, 5, 22, 49]
[41, 30, 57, 24, 53, 48, 35, 64]
[56, 59, 42, 29, 38, 23, 50, 47]
[43, 40, 61, 54, 45, 52, 63, 36]
[60, 55, 44, 39, 62, 37, 46, 51]

1
2
3
4
5
6
7
8
9
10

TIP

代码上有一个 next1 函数，就是因为查找的策略不同，从 0~7 这个策略，直接几分钟都没有反应。我以为是我默写实现的代码有 bug，把视频中老师的代码一个一个对比，没有发现有什么不同。

最后发现是查找下一个可以访问位置的策略不同，导致出现回溯太多，耗时太长

# 算法优化

第一种方式已经看到了，很慢很慢，慢的原因是：在顶层可回溯的太多了，比如：当前这个点可以有 8 个点可以走，下一个点还是有 8 个点可以走，那么随着递归的深入，就差不多是这样的：

10,9,8,7,6,5,4。。。  到最后可选的点最少

想一想，走到最后发现不能完成任务，就开始回溯，最前面可选择又很多，那么回溯就会变得更多。

想办法优先把选择少的先走。这里就可以使用 贪心算法（greedyalgorithm） 来对马儿走的策略进行优化。

我们这样做：对 next 返回的可走的点（的下一个可选择点的数量）进行 非递减 排序。也就是说先把选择少的先走

# 什么是非递减？

递增排序：1，2，3，4，5，6，...
递减排序：...6，5，4，3，2，1
非递减排序：1，2，2，3，4，5，...

升序排列？？
非递增排序：..6，6，5，5，3，2，1

看上去难道不就是升序吗？

# 代码实现

    /**
     * 贪心算法优化：按每一个点的 next 可选择的点数量进行升序排列
     *
     * @param points
     */
    private void sort(ArrayList<Point> points) {
        points.sort((o1, o2) -> {
            ArrayList<Point> next1 = next(o1);
            ArrayList<Point> next2 = next(o2);
            // 你可以尝试修改下这里：按降序排列的话，这个等待时间就太多了
            // 升序排列，我这里只需要 100 毫秒左右，而降序排列需要接近 1 分多钟甚至几分钟
            if (next1.size() > next2.size()) {
                return 1;
            } else if (next1.size() == next2.size()) {
                return 0;
            } else {
                return -1;
            }

        });
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

以上方法添加的时机为

        // 3. 根据当前节点计算马儿可以走的点
        ArrayList<Point> points = next(new Point(cx, cy));
				// 对选择进行优化，优先选择可选的点少的走
        sort(points);
        //  不为空则可以一直尝试走
        while (!points.isEmpty()) {
            Point point = points.remove(0);
            // 如果该点，没有被访问过，则递归访问：深度优先
            if (!visited[buildVisitedIndex(point.x, point.y)]) {
                traversalChessboard(chessboard, point.x, point.y, step + 1);
            }
        }

1
2
3
4
5
6
7
8
9
10
11
12

测试输出

耗时：104毫秒
耗时：0秒
[1, 16, 35, 32, 3, 18, 37, 22]
[34, 31, 2, 17, 36, 21, 4, 19]
[15, 52, 33, 46, 57, 62, 23, 38]
[30, 45, 60, 63, 54, 47, 20, 5]
[51, 14, 53, 56, 61, 58, 39, 24]
[44, 29, 64, 59, 48, 55, 6, 9]
[13, 50, 27, 42, 11, 8, 25, 40]
[28, 43, 12, 49, 26, 41, 10, 7]

1
2
3
4
5
6
7
8
9
10

← 弗洛伊德算法