# 克鲁斯卡尔算法
# 应用场景-公交站问题
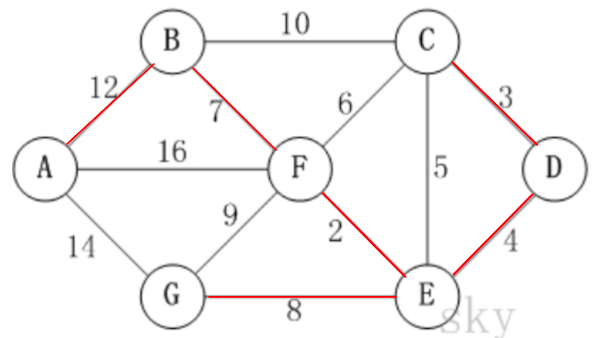
某城市新增 7 个站点(A, B, C, D, E, F, G) ，现在 需要修路把 7 个站点连通，各个站点的距离用边线表示(权) ，比如 A – B 距离 12公里 问：如何修路保证 各个站点都能连通，并且 总的修建公路总里程最短?
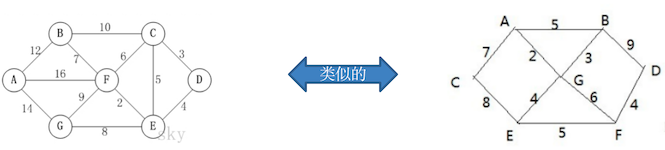
如上图所示：要求和前面的普利姆算法中的修路问题是一样的要求，只是换了一个背景。
# 克鲁斯卡尔算法介绍
克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。
基本思想：按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路
具体做法：
- 首先构造一个只含 n 个顶点的森林
- 然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止
# 克鲁斯卡尔算法图解
在含有 n 个顶点的连通图中选择 n-1 条边，构成一棵极小连通子图，并使该连通子图中 n-1 条边上权值之和达到最小，则称其为连通网的最小生成树。
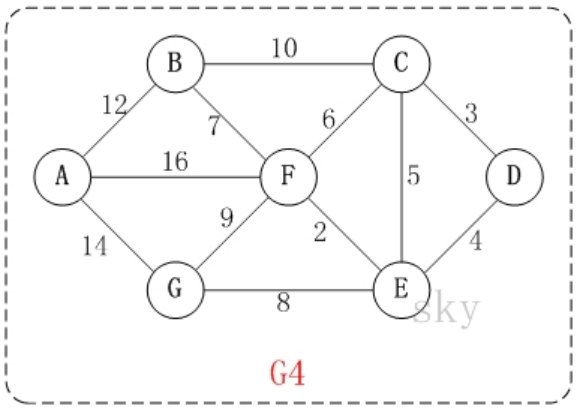
例如，对于如上图 G4 所示的连通网可以有多棵权值总和不相同的生成树。
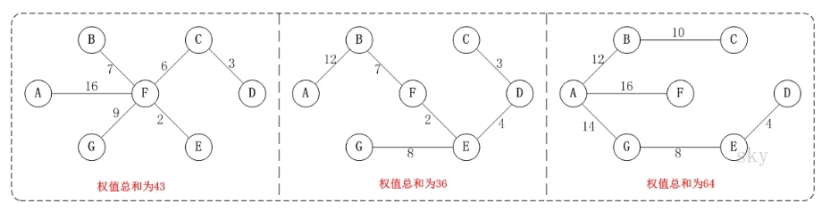
有多种不同的连通方式，但是哪一种权值才是最优的呢？下面是克鲁斯卡尔算法的图解步骤：
以上图 G4 为例，来对克鲁斯卡尔进行演示(假设，用数组 R 保存最小生成树结果)。
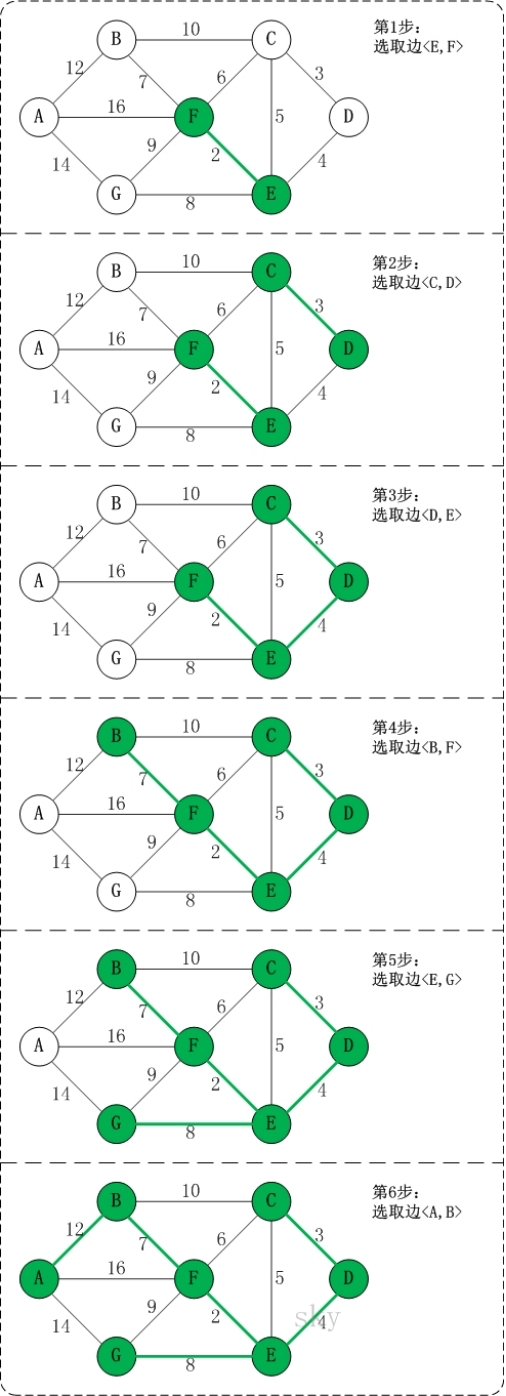
第 1 步：将边
E,F [2]加入 R 中。边
E,F的权值最小，因此将它加入到最小生成树结果 R 中。第 2 步：将边
C,D [3]加入 R 中。上一步操作之后，边
C,D的权值最小，因此将它加入到最小生成树结果 R 中。第 3 步：将边
D,E [4]加入 R 中。同理，权值最小
第 4 步：将边
B,F [7]加入 R 中。上一步操作之后，边
C,E [5]的权值最小，但C,E会和已有的边构成回路；因此，跳过边C,E。同理，跳过边C,F [6]。将边B,F加入到最小生成树结果R中。第 5 步：将边
E,G [8]加入 R 中。 同理第 6 步：将边
A,B [12]加入 R 中。上一步操作之后，边
F,G [9]的权值最小，但F,G会和已有的边构成回路；因此，跳过边F,G。同理，跳过边B,C [10]。将边A,B加入到最小生成树结果R中。 此时，最小生成树构造完成！它包括的边依次是：<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>总里程为 36。
# 克鲁斯卡尔算法分析
根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题：
对图的所有边按照权值大小进行排序。
此问题采用排序算法进行排序即可
将边添加到最小生成树中时，怎么样 判断是否形成了回路。
处理方式是：记录顶点在 最小生成树 中的终点，顶点的终点是 在最小生成树中与它连通的最大顶点。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。
# 如何判断回路？
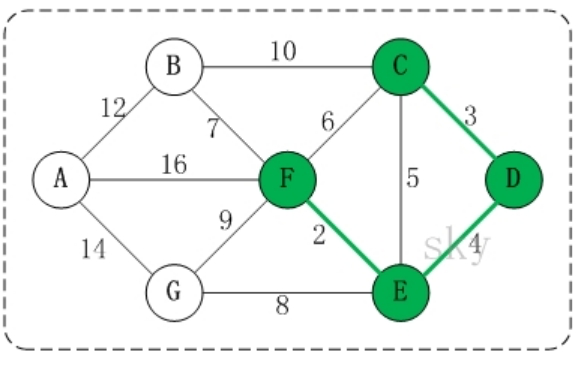
在将 E,F、 C,D D,E 加入到最小生成树 R 中之后，这几条边的顶点就都有了终点：
- C 的终点是 F。
- D 的终点是 F。
- E 的终点是 F。
- F 的终点是 F。
终点的说明：（备注：光看这个没有接触过该算法的不明白，在代码后面有详细的解释）
就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是 与它连通的最大顶点。
难道是说 CD、DE、EF 他们是一条线，从小到大，所以他们的终点都是 F?
因此，接下来，虽然
C,E是权值最小的边。但是 C 和 E 的终点都是 F，即它们的终点相同，因此，将C,E加入最小生成树的话，会形成回路。这就是判断回路的方式。也就是说，我们加入的边的两个顶点 不能都指向同一个终点，否则将构成回路。【后面有代码说明】
# 代码实现
# 无向图构建
这里使用上一章的普利姆算法中实现的无向图构建，简单修改下
package cn.mrcode.study.dsalgtutorialdemo.algorithm.kruskal;
import org.junit.Test;
/**
* 克鲁斯而
*/
public class KruskalCase {
// 不连通的默认值：0 则代表同一个点
int INF = 100000;
/**
* 图：首先需要有一个带权的连通无向图
*/
class MGraph {
int vertex; // 顶点个数
int[][] weights; // 邻接矩阵
char[] datas; // 村庄数据
int edgeNum; // 共有多少条边
/**
* @param vertex 村庄数量， 会按照数量，按顺序生成村庄，如 A、B、C...
* @param weights 需要你自己定义好那些点是连通的，那些不是连通的
*/
public MGraph(int vertex, int[][] weights) {
this.vertex = vertex;
this.weights = weights;
this.datas = new char[vertex];
for (int i = 0; i < vertex; i++) {
// 大写字母 A 从 65 开始
datas[i] = (char) (65 + i);
}
// 计算有多少条边
for (int i = 0; i < weights.length; i++) {
/*
A B C D E F G
A 0 12 100000 100000 100000 16 14
B 12 0 10 100000 100000 7 100000
j = i + 1：比如:
i=0,j=1, 那么就是 A,B 从而跳过了 A,A
i=1,j=2, 那么就是 B,C 从而跳过了 B,A B,B
那么含义就出来了：跳过双向边的统计，也跳过自己对自己值得为 0 的统计
*/
for (int j = i + 1; j < weights.length; j++) {
if (weights[i][j] != INF) {
edgeNum++;
}
}
}
}
public void show() {
System.out.printf("%-8s", " ");
for (char vertex : datas) {
// 控制字符串输出长度：少于 8 位的，右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", datas[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
}
@Test
public void mGraphTest() {
int[][] weights = new int[][]{
// A B C D E F G
/*A*/ {0, 12, INF, INF, INF, 16, 14},
/*B*/ {12, 0, 10, INF, INF, 7, INF},
/*C*/ {INF, 10, 0, 3, 5, 6, INF},
/*D*/ {INF, INF, 3, 0, 4, INF, INF},
/*E*/ {INF, INF, 5, 4, 0, 2, 8},
/*F*/ {16, 07, INF, INF, 2, 0, 9},
/*G*/ {14, INF, INF, INF, 8, 9, INF}
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
System.out.printf("共有 %d 条边", mGraph.edgeNum);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
测试输出
A B C D E F G
A 0 12 100000 100000 100000 16 14
B 12 0 10 100000 100000 7 100000
C 100000 10 0 3 5 6 100000
D 100000 100000 3 0 4 100000 100000
E 100000 100000 5 4 0 2 8
F 16 7 100000 100000 2 0 9
G 14 100000 100000 100000 8 9 100000
共有 12 条边
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
# 克鲁斯卡尔算法实现
/**
* 将无向图中的边 转换成对象数组
*
* @param graph
* @return
*/
public Edata[] convertEdatas(MGraph graph) {
Edata[] datas = new Edata[graph.edgeNum];
int[][] weights = graph.weights;
char[] vertexs = graph.datas;
int index = 0;
for (int i = 0; i < weights.length; i++) {
for (int j = i + 1; j < weights.length; j++) {
if (weights[i][j] != INF) {
datas[index++] = new Edata(vertexs[i], vertexs[j], weights[i][j]);
}
}
}
return datas;
}
/**
* 将边按权值从小到大排序
*
* @param edata
*/
public void sort(Edata[] edata) {
Arrays.sort(edata, Comparator.comparingInt(o -> o.weight));
}
public Edata[] kruskal(MGraph mGraph, Edata[] edatas) {
// 存放结果，数组最大容量为所有边的容量
Edata[] rets = new Edata[mGraph.edgeNum];
int retsIndex = 0;
/*
按照算法思路：
记录顶点在 **最小生成树** 中的终点，顶点的终点是 **在最小生成树中与它连通的最大顶点**。
然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。
*/
// 用于存所有的终点：该数组中的内容随着被选择的边增加，终点也会不断的增加
int[] ends = new int[mGraph.edgeNum];
// 对所有边进行遍历
for (Edata edata : edatas) {
// 获取这两条边的顶点下标:
// 第一次：E,F -> 4,5
int p1 = getPosition(mGraph.datas, edata.start);
int p2 = getPosition(mGraph.datas, edata.end);
// 获取对应顶点的 终点
/*
第 1 次：E,F -> 4,5
ends = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
m: 获取 4 的终点：ends[4] 为 0，说明此点 还没有一个终点，那么就返回它自己 4
n: 获取 5 的终点：同上
m != n , 选择这一条边。那么此时 E,F -> 4,5 已有边的终点就是 5
ends = [0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0]
终点表中读法： ↑ index=4,value=5 那么表示 4 这个顶点的终点为 5
第 2 次：C,D -> 2,3
ends = [0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0]
m: 获取 2 的终点，ends[2] = 0，说明此点 还没有一个终点，则返回它自己 2
n: 获取 3 的终点
m != n , 选择这一条边。那么此时 C,D -> 2,3 已有边的终点就是 3
ends = [0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]
第 3 次：D,E -> 3,4
ends = [0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]
m: 获取 3 的终点，ends[3] = 0，说明此点 还没有一个终点，则返回它自己 3
n: 获取 4 的终点,!! 前面第一次，已经将 4 的终点 5 放进来了
那么将获取到的终点为 5，getEnd() 还会尝试去获取 5 的终点，发现为 0，则 4 的终点是 5
m != n -> 3 != 5 , 选择这一条边。那么此时 D,E -> 3,4 已有边的终点就是 5
ends = [0, 0, 3, 5, 5, 0, 0, 0, 0, 0, 0, 0]
*/
int m = getEnd(ends, p1);
int n = getEnd(ends, p2);
if (m != n) {
ends[m] = n;
rets[retsIndex++] = edata;
}
}
return rets;
}
/**
* 获取该顶点的：终点
*
* @param ends
* @param vertexIndex
* @return
*/
private int getEnd(int[] ends, int vertexIndex) {
int temp = vertexIndex;
while (ends[temp] != 0) {
temp = ends[temp];
}
return temp;
}
/**
* 获取此顶点的下标
*
* @param vertexs
* @param vertex
* @return
*/
private int getPosition(char[] vertexs, char vertex) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == vertex) {
return i;
}
}
return 0;
}
/**
* 描述一条边
*/
class Edata {
// 一条边的开始和结束，比如 A,B
char start;
char end;
int weight; // 这条边的权值
public Edata(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return start + "," + end + " [" + weight + "]";
}
}
@Test
public void kruskalTest() {
int[][] weights = new int[][]{
// A B C D E F G
/*A*/ {0, 12, INF, INF, INF, 16, 14},
/*B*/ {12, 0, 10, INF, INF, 7, INF},
/*C*/ {INF, 10, 0, 3, 5, 6, INF},
/*D*/ {INF, INF, 3, 0, 4, INF, INF},
/*E*/ {INF, INF, 5, 4, 0, 2, 8},
/*F*/ {16, 07, INF, INF, 2, 0, 9},
/*G*/ {14, INF, INF, INF, 8, 9, INF}
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
System.out.printf("共有 %d 条边 \n", mGraph.edgeNum);
System.out.println("边数组为：");
Edata[] edatas = convertEdatas(mGraph);
printEdatas(edatas);
System.out.println("排序后的边数组为：");
sort(edatas);
printEdatas(edatas);
Edata[] kruskal = kruskal(mGraph, edatas);
System.out.println("克鲁斯卡尔算法计算结果的边为：");
printEdatas(kruskal);
int total = Arrays.stream(kruskal).filter(item -> item != null).mapToInt(item -> item.weight).sum();
System.out.println("总里程数为：" + total);
}
private void printEdatas(Edata[] edatas) {
for (Edata edata : edatas) {
if (edata == null) {
continue;
}
System.out.println(edata);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
测试输出
A B C D E F G
A 0 12 100000 100000 100000 16 14
B 12 0 10 100000 100000 7 100000
C 100000 10 0 3 5 6 100000
D 100000 100000 3 0 4 100000 100000
E 100000 100000 5 4 0 2 8
F 16 7 100000 100000 2 0 9
G 14 100000 100000 100000 8 9 100000
共有 12 条边
边数组为：
A,B [12]
A,F [16]
A,G [14]
B,C [10]
B,F [7]
C,D [3]
C,E [5]
C,F [6]
D,E [4]
E,F [2]
E,G [8]
F,G [9]
排序后的边数组为：
E,F [2]
C,D [3]
D,E [4]
C,E [5]
C,F [6]
B,F [7]
E,G [8]
F,G [9]
B,C [10]
A,B [12]
A,G [14]
A,F [16]
克鲁斯卡尔算法计算结果的边为：
E,F [2]
C,D [3]
D,E [4]
B,F [7]
E,G [8]
A,B [12]
总里程数为：36
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 获取一个点的终点解释
/**
* 获取该顶点的：终点
*
* @param ends
* @param vertexIndex
* @return
*/
private int getEnd(int[] ends, int vertexIndex) {
int temp = vertexIndex;
while (ends[temp] != 0) {
temp = ends[temp];
}
return temp;
}
....
int p1 = getPosition(mGraph.datas, edata.start);
int p2 = getPosition(mGraph.datas, edata.end);
int m = getEnd(ends, p1);
int n = getEnd(ends, p2);
if (m != n) {
ends[m] = n;
rets[retsIndex++] = edata;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
第 1 次：E,F -> 4,5
ends = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
m: 获取 4 的终点：ends[4] 为 0，说明此点 还没有一个终点，那么就返回它自己 4
n: 获取 5 的终点：同上
m != n , 选择这一条边。那么此时 E,F -> 4,5 已有边的终点就是 5
ends = [0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0]
终点表中读法： ↑ index=4,value=5 那么表示 4 这个顶点的终点为 5
第 2 次：C,D -> 2,3
ends = [0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0]
m: 获取 2 的终点，ends[2] = 0，说明此点 还没有一个终点，则返回它自己 2
n: 获取 3 的终点
m != n , 选择这一条边。那么此时 C,D -> 2,3 已有边的终点就是 3
ends = [0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]
第 3 次：D,E -> 3,4
ends = [0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]
m: 获取 3 的终点，ends[3] = 0，说明此点 还没有一个终点，则返回它自己 3
n: 获取 4 的终点,!! 前面第一次，已经将 4 的终点 5 放进来了
那么将获取到的终点为 5，getEnd() 还会尝试去获取 5 的终点，发现为 0，则 4 的终点是 5
m != n -> 3 != 5 , 选择这一条边。那么此时 D,E -> 3,4 已有边的终点就是 5
ends = [0, 0, 3, 5, 5, 0, 0, 0, 0, 0, 0, 0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
从以上的步骤运行来看，这个终点的判定是这样的：
E,F -> 4,5由于 终点列表中没有，那么第一条边的 起点 E 的终点就是 F记为：
ends = [0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 0, 0] 终点表中读法： ↑ index=4,value=5 那么表示 4 这个顶点的终点为 51
2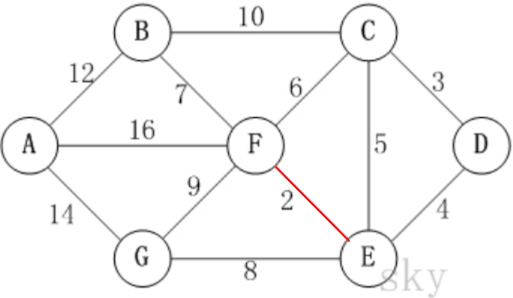
C,D -> 2,3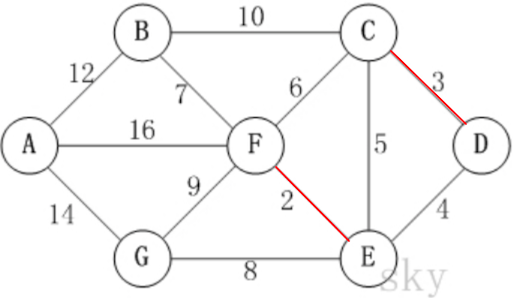
[0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]1选择这一条边后，终点列表中成了上面这样，如何理解？ 看上图：这两条边添加之后，他们并不能连通，所以此时的 ends 列表里面的含义就是这样的：
- 2：3 ， C 的终点是 D，因为这条边暂时没有和其他边连接
- 4：5，E 的终点是 F，因为这条吧暂时没有和其他边连接
D,E -> 3,4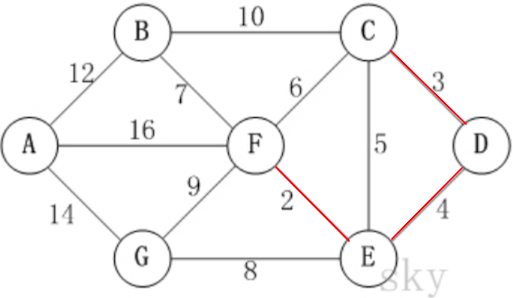
此时：可以看到，加入我们要选择这条边，那么 DE 就会和 EF 相连，获取边的终点时
[0, 0, 3, 0, 5, 0, 0, 0, 0, 0, 0, 0]1先获取 D 的终点：
ends[3]=0，返回它自己；获取 E 的终点时：
edns[4]=5，你会发现，其实 E 它已经和 F 连通了那么此时：往终点列表里面存放的则是 D 的终点是 F，而不是 E
ends = [0, 0, 3, 5, 5, 0, 0, 0, 0, 0, 0, 0]1
最终选择完后的终点列表中的数据为
[6, 5, 3, 5, 5, 6, 0, 0, 0, 0, 0, 0] A B C D E F G 0 1 2 3 4 5 61
2
3- A 的终点是 G
- B 的终点是 F → G
- C 的终点是 D → F → G
- D 的终点是 F → G
- E 的终点是 F → G
- F 的终点是 G
选择看明白了吗？它利用这一个数组，对于每次新增的边 和 已经存在的边，计算出，新增加的边的起始点，对应的终点是什么。 当整个最小生成树都完成的时候，他们最终所对应的终点都是一样的。