# 弗洛伊德算法
# 介绍
和 Dijkstra 算法一样，弗洛伊德(Floyd)算法 也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名
弗洛伊德算法(Floyd)计算图中 各个顶点之间 的最短路径，比如：先从 A 出发到各个点的最短路径，再从 B 出发，直到所有节点距离各个点的路径都会计算出来。而迪杰斯特拉算法用于计算图中 某一个顶点到其他顶点的最短路径。
弗洛伊德算法 VS 迪杰斯特拉算法：
- 迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径；
- 弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径。
# 核心思想
设：
- 顶点 vi 到顶点 vk 的最短路径已知为Lik，
- 顶点 vk 到 vj 的最短路径已知为 Lkj
- 顶点 vi 到 vj 的路径为 Lij
则 vi 到 vj 的最短路径为：min((Lik+Lkj),Lij)，vk 的取值为图中所有顶点，则可获得 vi 到 vj 的最短路径（则：假设三个点（不一定是具体的是 3 个点），一个直达，一个间接到达，算哪个路径最短）
至于 vi 到 vk 的最短路径 Lik 或者 vk 到 vj 的最短路径 Lkj，是以同样的方式获得
# 图解
以前面的公交站距离图解
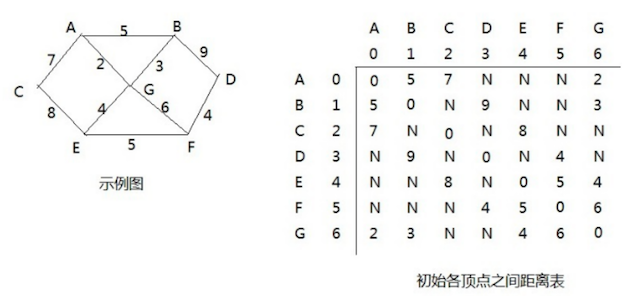
上图中含义：
- 0：表示自己与自己。如 A,A
- N：表示不可直连
初始前驱顶点如上图：每个节点到达其他节点的初始前驱都是它自己。
第一轮循环中，以 A (下标为：0) 作为 中间顶点，距离表和前驱关系更新为：
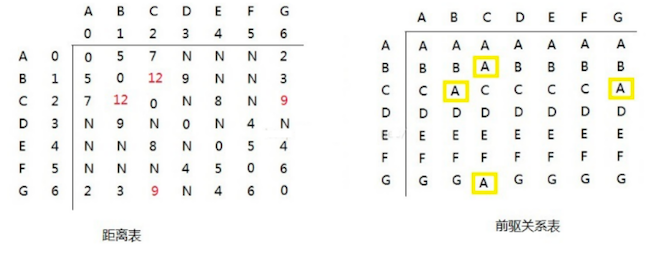
找出以 A 为中间顶点的路径：
C-A-G：距离为 9C-A-B：距离为 12G-A-B：距离为 7
因为图是无向的，只需要计算一个方向的即可。
更新距离表，需要与上一次的距离表作为参照对比
C-A-G：距离为 9，原始C,G距离为 N，9 < N，则更新C,G = 9C-A-B：距离为 12，原始C,B距离为 N，12 < N，则更新C,B=12G-A-B：距离为 7，原始G,B距离为 3，则不更新
另外由于是无向图，更新其中一个，那么另外一个方向的也要同步更新。
同时：更新对应位置的前驱节点为 A
如何找出以 A 为中间顶点的所有路径？
// 使用 3 个数组来实现，思路如下 中间顶点：[A,B,C,D,E,F,G] k=0 出发顶点：[A,B,C,D,E,F,G] i=0,1.... 终点顶点：[A,B,C,D,E,F,G] j=0,1,2... 以 k 为中间顶点时，使用一个双层循环,来遍历出所有的情况 并在这个寻找路径的循环中，找出最短路径，去更新上述所演示的：距离表、前驱表1
2
3
4
5
6
7当把 A 作为中间顶点路径寻找完成之后，表中的数据则为 A 到所有顶点的最短距离。
当所有顶点都更新之后，最后就是每个顶点到其他顶点的最短距离（注：所有顶点没有更新完成之前，最终结果不一定是最短的，后续可能还会更新）
看上去很简单，就是一个三层 for 循环，但是它的时间复杂度是 n3，比如这里有 7 个节点，那么循环的次数是
7x7x7=343
# 弗洛伊德算法最佳应用-最短路径
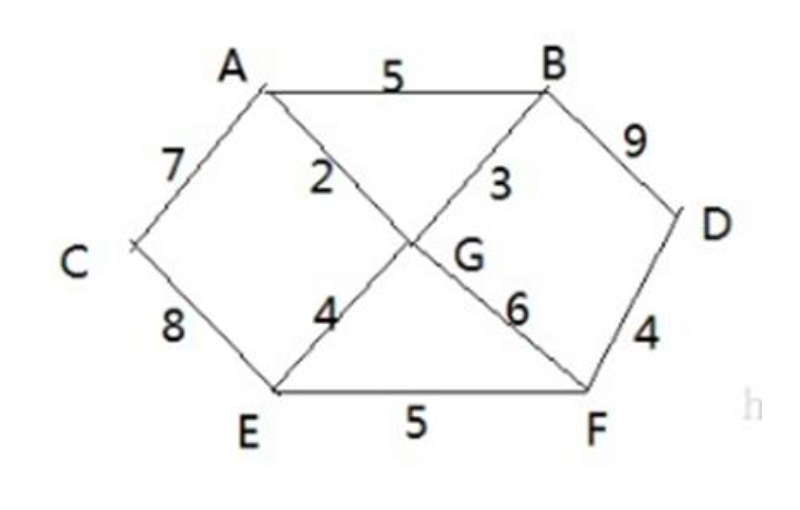
胜利乡有 7 个村庄 (A, B, C, D, E, F, G)，各个村庄的距离用边线表示（权），比如 A-B 距离为 5 公里
问：如何计算出 各村庄到其他各村庄的最短距离？
下面直接用代码实现，前面图解和思路都说了。
# 准备工作
主要做了 3 件事情：
- 复用了之前的无向图和打印功能
- 初始化弗洛伊德算法中用到的 3 个数组和初始化
- 打印状态和结果
package cn.mrcode.study.dsalgtutorialdemo.algorithm.floyd;
import org.junit.Test;
import java.util.Arrays;
/**
* 佛洛依德算法-最短路径
*/
public class FloydAlgorithm {
/**
* 图：首先需要有一个带权的连通无向图
*/
class MGraph {
int vertex; // 顶点个数
int[][] weights; // 邻接矩阵
char[] datas; // 村庄数据
/**
* @param vertex 村庄数量， 会按照数量，按顺序生成村庄，如 A、B、C...
* @param weights 需要你自己定义好那些点是连通的，那些不是连通的
*/
public MGraph(int vertex, int[][] weights) {
this.vertex = vertex;
this.weights = weights;
this.datas = new char[vertex];
for (int i = 0; i < vertex; i++) {
// 大写字母 A 从 65 开始
datas[i] = (char) (65 + i);
}
}
public void show() {
System.out.printf("%-8s", " ");
for (char vertex : datas) {
// 控制字符串输出长度：少于 8 位的，右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", datas[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
}
@Test
public void mGraphTest() {
// 不连通的默认值：
// 这里设置为较大的数，是为了后续的计算方便，计算权值的时候，不会选择
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
}
@Test
public void floydTest() {
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
floyd(mGraph);
showFloydDis();
showFloydPre();
showFormat();
}
private char[] vertexs; // 存放顶点
private int[][] dis; // 从各个顶点出发到其他顶点的距离
private int[][] pre; // 到达目标顶点的前驱顶点
public void floyd(MGraph mGraph) {
vertexs = mGraph.datas;
dis = mGraph.weights;
pre = new int[mGraph.vertex][mGraph.vertex];
// 初始化 pre
for (int i = 0; i < pre.length; i++) {
Arrays.fill(pre[i], i);
}
}
/**
* 显示 dis 和 pre，这个数据也是最后的结果数据
*/
public void showFloydDis() {
System.out.println("dis 结果");
show(dis);
}
public void showFloydPre() {
System.out.println("pre 结果");
show(pre);
}
public void show(int[][] weights) {
System.out.printf("%-8s", " ");
for (char vertex : vertexs) {
// 控制字符串输出长度：少于 8 位的，右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", vertexs[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
/**
* 直接打印出我们的结果
*/
public void showFormat() {
System.out.println("最终结果格式化显示：");
for (int i = 0; i < dis.length; i++) {
// 先将 pre 数组输出一行
System.out.println(vertexs[i] + " 到其他顶点的最短距离");
// 输出 dis 数组的一行数据
// 每一行数据是，一个顶点，到达其他顶点的最短路径
for (int k = 0; k < dis.length; k++) {
System.out.printf("%-16s", vertexs[i] + " → " + vertexs[k] + " = " + dis[i][k] + "");
}
System.out.println();
System.out.println();
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
测试输出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
dis 结果
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
pre 结果
A B C D E F G
A 0 0 0 0 0 0 0
B 1 1 1 1 1 1 1
C 2 2 2 2 2 2 2
D 3 3 3 3 3 3 3
E 4 4 4 4 4 4 4
F 5 5 5 5 5 5 5
G 6 6 6 6 6 6 6
最终结果格式化显示：
A 到其他顶点的最短距离
A → A = 100000 A → B = 5 A → C = 7 A → D = 100000 A → E = 100000 A → F = 100000 A → G = 2
B 到其他顶点的最短距离
B → A = 5 B → B = 100000 B → C = 100000 B → D = 9 B → E = 100000 B → F = 100000 B → G = 3
C 到其他顶点的最短距离
C → A = 7 C → B = 100000 C → C = 100000 C → D = 100000 C → E = 8 C → F = 100000 C → G = 100000
D 到其他顶点的最短距离
D → A = 100000 D → B = 9 D → C = 100000 D → D = 100000 D → E = 100000 D → F = 4 D → G = 100000
E 到其他顶点的最短距离
E → A = 100000 E → B = 100000 E → C = 8 E → D = 100000 E → E = 100000 E → F = 5 E → G = 4
F 到其他顶点的最短距离
F → A = 100000 F → B = 100000 F → C = 100000 F → D = 4 F → E = 5 F → F = 100000 F → G = 6
G 到其他顶点的最短距离
G → A = 2 G → B = 3 G → C = 100000 G → D = 100000 G → E = 4 G → F = 6 G → G = 100000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
可以看到如上的输出，能方便我们查看状态图。
# 弗洛伊德算法核心代码
就是三层循环处理
public void floyd(MGraph mGraph) {
vertexs = mGraph.datas;
dis = mGraph.weights;
pre = new int[mGraph.vertex][mGraph.vertex];
// 初始化 pre
for (int i = 0; i < pre.length; i++) {
Arrays.fill(pre[i], i);
}
// 从中间顶点的遍历
for (int i = 0; i < vertexs.length; i++) {
// 出发顶点
for (int j = 0; j < vertexs.length; j++) {
// 终点
for (int k = 0; k < vertexs.length; k++) {
// 中间节点连接: 从 j 到 i 到 k 的距离
int lji = dis[j][i];
int lik = dis[i][k];
int leng = lji + lik;
// 直连
int ljk = dis[j][k];
// 如果间接距离比直连短，则更新
if (leng < ljk) {
dis[j][k] = leng;
/*
最难理解的是这里：
i 是已知的中间节点，前驱的时候直接设置为 i (pre[j][k] = i;) ，结果是不对的。
比如：A-G-F-D ， 中间节点是是 两个节点，那么 A 到 D 的前驱节点是 F，而不是 G
如果直接赋值 i，前驱节点就会计算错误。
理解步骤为：
1. A-G-F：距离 8
A-F : 不能直连
那么设置：A,F 的前驱节点是 G; 对应这里的代码是 j,i
2. G-F-D: 距离是 10
G-D：不能直连
那么设置：G,D 的前驱节点是 F; 对应这里的代码是 i,k
3. 那么最终 A,D 的前驱节点是是什么呢？
其实就应该是 G,D 指向的值; 对应这里的代码是 i,k
*/
pre[j][k] = pre[i][k]; // 前驱节点更新为中间节点
}
}
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
测试输出结果
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
dis 结果
A B C D E F G
A 4 5 7 12 6 8 2
B 5 6 12 9 7 9 3
C 7 12 14 17 8 13 9
D 12 9 17 8 9 4 10
E 6 7 8 9 8 5 4
F 8 9 13 4 5 8 6
G 2 3 9 10 4 6 4
pre 结果
A B C D E F G
A 6 0 0 6 6 6 0
B 1 6 0 1 6 6 1
C 2 0 0 5 2 4 0
D 6 3 5 5 5 3 5
E 6 6 4 5 6 4 4
F 6 6 4 5 5 3 5
G 6 6 0 5 6 6 0
最终结果格式化显示：
A 到其他顶点的最短距离
A → A = 4 A → B = 5 A → C = 7 A → D = 12 A → E = 6 A → F = 8 A → G = 2
B 到其他顶点的最短距离
B → A = 5 B → B = 6 B → C = 12 B → D = 9 B → E = 7 B → F = 9 B → G = 3
C 到其他顶点的最短距离
C → A = 7 C → B = 12 C → C = 14 C → D = 17 C → E = 8 C → F = 13 C → G = 9
D 到其他顶点的最短距离
D → A = 12 D → B = 9 D → C = 17 D → D = 8 D → E = 9 D → F = 4 D → G = 10
E 到其他顶点的最短距离
E → A = 6 E → B = 7 E → C = 8 E → D = 9 E → E = 8 E → F = 5 E → G = 4
F 到其他顶点的最短距离
F → A = 8 F → B = 9 F → C = 13 F → D = 4 F → E = 5 F → F = 8 F → G = 6
G 到其他顶点的最短距离
G → A = 2 G → B = 3 G → C = 9 G → D = 10 G → E = 4 G → F = 6 G → G = 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 关于前驱节点的计算
核心代码中有下面这样一段注释
i 是已知的中间节点，前驱的时候直接设置为 i (pre[j][k] = i;) ，结果是不对的。
比如：A-G-F-D ， 中间节点是是 两个节点，那么 A 到 D 的前驱节点是 F，而不是 G
如果直接赋值 i，前驱节点就会计算错误。
理解步骤为：
1. A-G-F：距离 8
A-F : 不能直连
那么设置：A,F 的前驱节点是 G; 对应这里的代码是 j,i
2. G-F-D: 距离是 10
G-D：不能直连
那么设置：G,D 的前驱节点是 F; 对应这里的代码是 i,k
3. 那么最终 A,D 的前驱节点是是什么呢？
其实就应该是 G,D 指向的值; 对应这里的代码是 i,k
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
对于上面的描述，下面用图例解释下
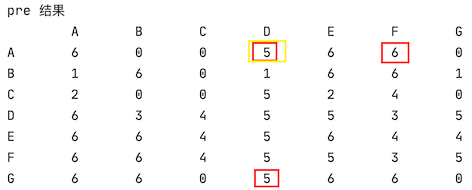
A-G-F，设置 A 到达 F 的前驱是 G，
A,F = 6，上图中的下标 6 就是 G这个是正确的
G-F-D，设置 G 到达 D 的前驱是 F，
G,D = 5，上图中的下标 5 就是 F那么 A-G-F-D，设置 A 到达 D 的前驱是 ?
这里需要这样来看
A - G-F-D A - X 把 A-G-F-D 看成 A-X 而 X=G-F-D G-F-D, 的前驱节点是 F 则 A-X 的前驱节点是 F 则 A-D 的前驱节点是 F1
2
3
4
5
6
7