# 快速排序
# 简单介绍
Quicksort 快速排序 是对 冒泡排序的一种改进。
# 基本思想
通过一趟排序将要排序的数据 分割成独立的两个部分,一部分的所有数据都比另外一部分的所有数据都要小。
然后再按如上的方法对这两部分数据分别进行快速排序,排序过程可以递归进行,以此达到整个数据变成有序序列。
比如如下的示意图:
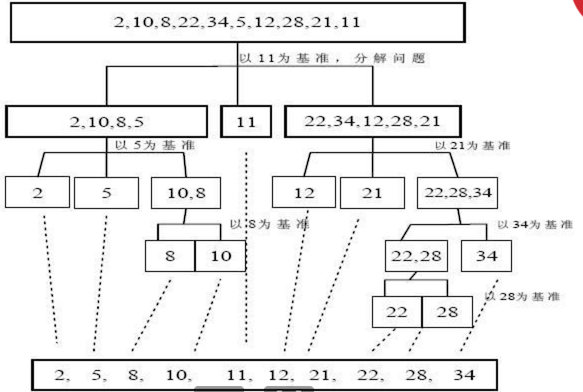
- 上图以 最后一个元素的值 作为基准
- 比基准值小的,排在左侧,比基准值大的排在右侧
- 然后再以分好的部分重复以上操作,直到每个部分中只有一个数据时,就排好序了
# 思路分析
基本思想如上,但是实现思路有多种,这里不以上图那样用数组元素最后一个为基准值,这里使用 数组中间 的作为基准值,进行讲解
如下图

- 挑选的基准值为数组中间的值
- 中间值就把数组分成了两组
- 左边一组,从左到右,挨个与 基准值 比较,找出比基准值大的值
- 右边一组,从右到左,挨个与 基准值 比较,找出比基准值小的值
- 左右两边各找到一个值,那么就让这两个值进行交换
- 然后继续找,直到左右两边碰到,这一轮就结束。这一轮就称为快速排序
- 继续对分出来的小组,进行上述的快速排序操作,直到组内只剩下一个数时,则排序完成
l ------------ pivot --------------- r
一组从左往右找 一组从右往左找
1
2
2
可以看到,分组后,可以使用递归,对这一组继续分组,然后对他们进行快速排序。
# 代码实现
# 推导实现
推导法先实现第一轮
@Test
public void processDemo() {
int arr[] = {-9, 78, 0, 23, -567, 70};
System.out.println("原始数组:" + Arrays.toString(arr));
processQuickSort(arr, 0, arr.length - 1);
}
/**
* @param arr
* @param left 左变这一组的下标起始点,到中间值,则为一组
* @param right 右边这一组的下标结束点,到中间值,则为一组
*/
public void processQuickSort(int[] arr, int left, int right) {
/*
基本思想:选择一个基准值,将基准值小分成一组,比基准值大的分成一组。
这里的实现思路:
1. 挑选的基准值为数组中间的值
2. 中间值就把数组分成了两组
3. 左边一组,从左到右,挨个与 基准值 比较,找出比基准值大的值
4. 右边一组,从右到左,挨个与 基准值 比较,找出比基准值小的值
5. 左右两边各找到一个值,那么就让这两个值进行交换
6. 然后继续找,直到左右两边碰到,这一轮就结束。这一轮就称为快速排序
7. 继续对分出来的小组,进行上述的快速排序操作,直到组内只剩下一个数时,则排序完成
l ------------ pivot --------------- r
一组从左往右找 一组从右往左找
*/
int l = left;
int r = right;
// 中心点,让这个点作为基准值
int pivot = arr[(left + right) / 2];
// 当他们没有碰到的时候,说明还这一轮还可以继续找
while (l < r) {
// 左边:当找到大于基准值时,则表示该值需要交换到右侧去: arr[l] > pivot
// 也就是说,如果 arr[l] < pivot,则表示还没有找到比基准值大的数
// 注意:不能等于 pivort,因为最差的情况没有找到,则最后 arr[l] 就是 pivot 这个值,那么就会出现死循环
while (arr[l] < pivot) {
l++; // 所以让左边这一组继续找
}
// 右边:当找到小于基准值时,则表示该值需要交换到左侧去:arr[r] < pivot
// 那么这里和上面的相反
while (arr[r] > pivot) {
r--;
}
// 当左侧与右侧相碰时,说明两边都没有找到,这一轮比进行交换
// 等于表示,找到了中间的下标
if (l >= r) {
break;
}
// 当找到时,则进行交换
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
// 当交换后,
// 当数组是: {-9, 78, 0, -23, 0, 70} 时,就可以验证这里的逻辑
// 如果没有这个判定,将会导致,l 永远 小于 r。循环不能退出来的情况
if (arr[l] == pivot) {
/*
不能让自己往前移动 1,因为当交换完成后为:{-9, 0, 0, -23, 78, 70}
l = 1, = 0
r = 4, = 78
如果 l 等于 2,那么相当于下一轮,基准值 - 将会与 -23 进行交换,导致基准值变化了
所以,让 r - 1,还有一个原因是,r 是刚刚交换过的,一定比 基准值大,所以没有必要再和基准值比较了
*/
r -= 1;
}
// 这里和上面一致,如果说,先走了上面的 r-=1
// 这里也满足,那么说明,下一次是相同的两个值,一个是 r 一个是基准值(满足条件 l+1 了,所以就有可能指向了基准值),进行交换
// 但是他们是相同的值,交换后,不影响。但是再走这完这里逻辑时,就会导致 l > r,循环退出
if (arr[r] == pivot) {
l += 1;
}
}
System.out.println("第 1 轮排序后:" + Arrays.toString(arr));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
注意:上述的算法特别是边界判定,就是上面「当交换后」对 r-=1 的这个边界判定时,有点难以理解,但是一定要理解为什么要这样写。
测试信息输出
原始数组:[-9, 78, 0, 23, -567, 70]
第 1 轮排序后:[-9, -567, 0, 23, 78, 70]
1
2
2
那么如何向左递归和右递归呢?在上面的代码后面接着实现如下
System.out.println("第 1 轮排序后:" + Arrays.toString(arr));
// 如果 l = r,会出现死循环
if (l == r) {
l++;
r--;
}
// 开始左递归
// 上面算法是 r--,l++ ,往中间走,当 left < r 时,表示还可以继续分组
if (left < r) {
processQuickSort(arr, left, r);
}
if (right > l) {
processQuickSort(arr, l, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 完整实现
完整实现和推导实现其实差不多了,为了加深记忆,自己按照基本思想和思路分析,默写。
/**
* 快速排序默写实现
* <pre>
* 基本思想:通过一趟将要排序的数据,分隔成独立的两个部分,一部分的所有数据都比另一部分的所有数据要小。
* 思路分析:
* {-9, 78, 0, 23, -567, 70}; length=6
* 1. 挑选中间的值作为 基准值:(0 + (6 -1))/2= [2] = 0
* 2. 左侧 left 部分,从 0 开始到中间值 -1: 0,1: -9, 78,找出一个比基准值大的数
* 3. 右侧 right 部分,从中间值 + 1 到数组大小-1:3,5:23,-567, 70,找出一个比基准值小的数
* 4. 如果找到,则将他们进行交换,这样一轮下来,就完成了一次快速排序:一部分的所有数据都比另一部分的所有数据要小。
* 4. 如果左侧部分还可以分组,则进行左侧递归调用
* 5. 如果右侧部分还可以分组,则进行右侧递归调用
*
* 简单说:一轮快速排序示意图如下:
* 中间的基准值
* l ------------ pivot --------------- r
* 一组从左往右找 一组从右往左找
* 找到比基准值大的数 找出一个比基准值小的数
* 然后进行交换
* </pre>
*/
@Test
public void quickSortTest() {
int arr[] = {-9, 78, 0, 23, -567, 70};
// int arr[] = {-9, 78, 0, -23, 0, 70}; // 在推导过程中,将会导致交换异常的数组,在这里不会出现那种情况
int left = 0;
int right = arr.length - 1;
System.out.println("原始数组:" + Arrays.toString(arr));
quickSort(arr, left, right);
System.out.println("排序后:" + Arrays.toString(arr));
}
public void quickSort(int[] arr, int left, int right) {
// 找到中间值
int pivotIndex = (left + right) / 2;
int pivot = arr[pivotIndex];
int l = left;
int r = right;
while (l < r) {
// 从左往右找,直到找到一个数,比基准值大的数
while (arr[l] < pivot) {
l++;
}
// 从右往左找,知道找到一个数,比基准值小的数
while (arr[r] > pivot) {
r--;
}
// 表示未找到
if (l >= r) {
break;
}
// 进行交换
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
// 那么下一轮,左侧的这个值将不再参与排序,因为刚交换过,一定比基准值小
// 那么下一轮,右侧的这个值将不再参与排序,因为刚交换过,一定比基准值大
r--;
l++;
}
// 当一轮找完后,没有找到,则是中间值时,
// 需要让他们插件而过,也就是重新分组,中间值不再参与分组
// 否则,在某些情况下,会进入死循环
if (l == r) {
l++;
r--;
}
// 如果左侧还可以继续分组,则继续快排
// 由于擦肩而过了,那么左侧的组值,则是最初的开始与中间值的前一个,也就是这里得到的 r
if (left < r) {
quickSort(arr, left, r);
}
if (right > l) {
quickSort(arr, l, right);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
另外,在实现的过程中,将某些代码为什么要那样判断边界,进行了梳理。你会发现上述代码和推导的代码有一定的差别。这个是笔者自己的改进,更容易看明白。目前未发现 bug
# 大数据量耗时测试
/**
* 大量数据排序时间测试
*/
@Test
public void bulkDataSort() {
int max = 80_000;
// int max = 8;
int[] arr = new int[max];
for (int i = 0; i < max; i++) {
arr[i] = (int) (Math.random() * 80_000);
}
if (arr.length < 10) {
System.out.println("原始数组:" + Arrays.toString(arr));
}
Instant startTime = Instant.now();
// processQuickSort(arr, 0, arr.length - 1); // 和老师的原版代码对比,结果是一样的
quickSort(arr, 0, arr.length - 1);
if (arr.length < 10) {
System.out.println("排序后:" + Arrays.toString(arr));
}
Instant endTime = Instant.now();
System.out.println("共耗时:" + Duration.between(startTime, endTime).toMillis() + " 毫秒");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
多次运行输出
共耗时:40 毫秒
共耗时:52 毫秒
共耗时:36 毫秒
共耗时:31 毫秒
1
2
3
4
2
3
4