# 聚合算法讲解
# 易并行算法 max
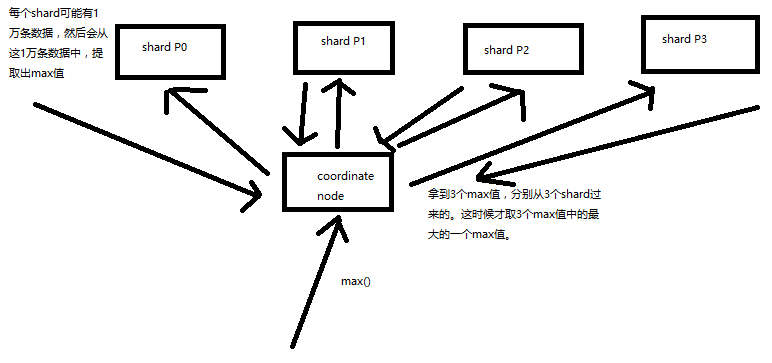
有些聚合分析的算法,是很容易就可以并行的,比如说 max,流程如下:
- 假设有 3 和 shard 查找最大值
- 每个 shard 查找并返回一个最大值
- 在聚合节点上会拿到 3 个值,然后在这三个值中排序出最大的一个即可
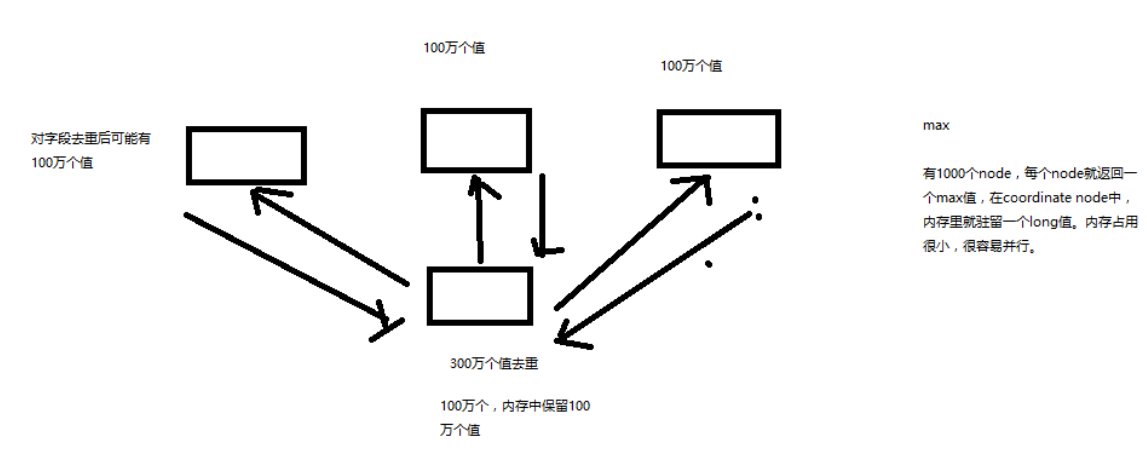
有些聚合分析的算法是不好并行的,比如说 count(distinct)(去重后统计剩余数量,也就是唯一值个数),
并不是说在每个 node 上直接就出一些 distinct value 就可以的,因为每个 shard 之间可能还有重复的数据,所以就不准的,
这个时候就需要从每个 shard 上把所有相关数据都获取过来,然后计算
如下图
不易并行算法进行聚合的时候,由于数据量可能太大会导致内存占用过多,性能严重影响,甚至内存溢出,
这个时候 es 会采取近似聚合的方式,就是采用在每个 node 上进行近估计的方式,
得到最终的结论,如:cuont(distcint) 本来是 100 万,可能会返回 105 万,
近似估计后的结果,不完全准确,但是速度会很快,一般会达到完全精准的算法的性能的数十倍。
这就会出现一个概念,三角选择原则
# 三角选择原则
精准 + 实时 + 大数据只能选择 2 个
- 精准+实时: 没有大数据,数据量很小,那么一般就是单机跑,随便你则么玩儿就可以
- 精准+大数据:hadoop 批处理,非实时,可以处理海量数据,保证精准,可能会跑几个小时
- 大数据+实时:es,不精准,近似估计,可能会有百分之几的错误率
# 近似聚合算法
- 如果采取近似估计的算法:延时在 100ms 左右,0.5% 错误
- 如果采取 100% 精准的算法:延时一般在 ns~几十s,甚至几十分钟,几小时, 0% 错误
TIP
对于这个错误率不知道是怎么出来的,就是一句话数据量非百分百准确